Microsoft Excel Поиск решения

Вирішення задач оптимізації за допомогою інструмента

Вступ

Київ 2010

УДК 681.3

ББК 32.973.26-018.2

С 40

Укладачі: Г.Л. Васильєва, канд. фіз.-мат. наук, доцент,

М. В. Коханович, старший викладач

Рецензент: О. Ю. Філімонова, канд.. техн.. наук, доцент

Відповідальний за випуск П.П.Лізунов, доктор техн. наук, професор

Затверджено на засіданні кафедри основ інформатики, протокол №___ від ___.___.2010 р.

Видається в авторській редакції.

С 40 Методичні вказівки до практичних робіт з навчальної дисципліни «Комп’ютерні технології економічних розрахунків» для студентів спеціальності 8.050201 «Менеджмент організацій» /Уклад.: Г.Л.Васильєва, М.В. Коханович. – К.: КНУБА, 2010. – с.

Призначено для студентів спеціальності 8.050201 «Менеджмент організацій»

Багато проблем виробництва, проектування, прогнозування зводиться до широкого класу задач оптимізації, для вирішення яких використовуються математичні методи.

Типовими задачами оптимізації є задачі на:

асортимент продукції – максимізація випуску товарів при наявності обмежень на сировину для виробництва товарів;

штатний розклад – складання штатного розкладу для досягнення найкращих результатів за найменших витрат;

планування перевезень – мінімізація витрат на транспортування товарів;

створення суміші – досягнення заданої якості суміші за найменших витрат;

та інші різноманітні задачі оптимального розподілення ресурсів та оптимального проектування.

В даних методичних вказівках розглядаються вирішення прикладів подібних задач з використання надбудови Поиск решения електронних таблиць Microsoft Excel.

Умови практичних задач оптимізації включають досягнення певної конкретної мети, наприклад знаходження мінімального рішення за існування певних обмежень вихідних даних. Специфіка таких задач полягає в тому, що створена математична модель досліджуваного процесу, але невідоме значення параметра, за якого можна досягти поставленої мети.

В Microsoft Excel вирішення подібних задач реалізовано як пошук значення параметра функції, що відповідає конкретному значенню функції. Таким чином, за допомогою Excel можна вирішувати будь-які системи рівнянь з одним невідомим. Можливо також знаходити значення кількох параметрів, що забезпечують отримання попередньо заданого результату. В окремих задачах треба знайти не конкретне значення параметра, а максимально чи мінімально можливе. Наприклад, визначення значення у даній ячейці, що відповідає екстремуму у залежній ячейці. Цільова та залежна клітинки повинні бути пов'язані формулою, щоб зміна числового значення в одній з них викликала зміну змісту іншої ячейки. Подібні задачі у Excel вирішуються за допомогою команди Сервис, Поиск решения.

Формулювання задачі оптимізації у загальному вигляді наведене у табл.1.

Таблиця 1. Постановка задачі оптимізації у загальному вигляді

№ пп.	Назва	Опис
	Цільова функція (критерій оптимізації)	Показує, в якому сенсі рішення повинно бути оптимальним, тобто найкращим. Можливі три типи цільової функції: максимізація, мінімізація, досягнення заданого значення.
	Обмеження	Встановлюють залежності між змінними. Можуть бути односторонніми та двосторонніми. Під час вирішення задачі двостороннє обмеження записується у вигляді двох односторонніх.
	Граничні умови	Показують у яких межах можуть знаходитись значення шуканих змінних у оптимальному рішенні.

Рішення задачі (табл. 1, пп. 1-3), що задовольняє всім обмеженням і граничним умовам, називається допустимим. Задача має оптимальне рішення, якщо вона задовольняє двом умовам:

v має більш, ніж одне рішення, тобто існують допустимі рішення;

v є критерій, що показує, у якому сенсі шукане рішення повинне бути оптимальним, тобто найкращим з можливих.

За допомогою інструмента Поиск решения у Microsoft Excel можливо вирішувати як лінійні задачі (задачі лінійного, цілочисельного і стохастичного програмування), так і нелінійні (задачі нелінійного програмування).

Надбудова Поиск решения запускається командою Сервис, Поиск решения. Якщо в меню Сервис відсутня команда Поиск решения, слід скористатися командою Сервис, Надстройки і встановити відповідний прапорець. Вигляд вікна Поиск решения наведений на рис. 1, а опції його налаштування у табл. 2.

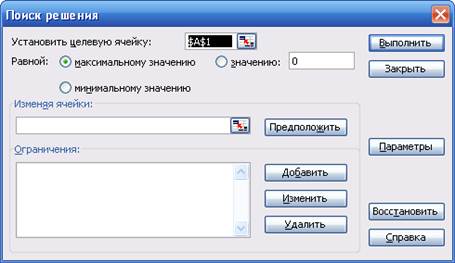
Рис. 1.

Таблиця 2. Опції вікна Поиск решения

№ пп.	Опції	Опис
	Установить целевую ячейку	Вказується клітинка, що містить цільову функцію (критерій оптимізації) розглядуваної задачі.
	Равной	Слід обрати з трьох перемикачів (максимальному значению, минимальному значению, значению) той, що визначає тип взаємозв’язку між рішенням і цільовою клітинкою.
	Изменяя ячейки	Вказуються клітинки, які повинні змінюватися у процесі пошуку рішення задачі, тобто клітинки, які є змінними задачі.
	Ограничения	Відображаються обмеження, що накладаються на змінні задачі. Допускаються обмеження у вигляді рівностей, нерівностей, а також – вимога цілочисельності змінних. Обмеження додаються по одному за допомогою кнопки Добавить.
	КнопкаПараметры	Дозволяє змінити умови та варіанти пошуку рішень досліджуваної задачі, а також завантажувати і зберігати оптимізовані моделі. Значення і стан елементів керування, що використовуються за умовчанням, є придатними для вирішення більшості задач.

При натисненні кнопки Параметры у вікні Поиск решения відкривається вікно Параметры поиска решения (рис. 2), опис опцій якого наведений у табл. 3.

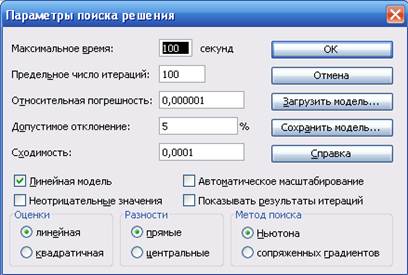
Рис. 2.

Таблиця 3. Опції вікна Параметры поиска решения

№ пп.	Опції	Опис
	Максимальное время	Обмежує час, що відпускається на пошук рішення задачі.
	Предельное число итераций	Обмежує кількість проміжних обчислень.
	Относительная погрешность	Визначає точність пошуку рішення. Після знаходження рішення з величинами параметрів, заданих за умовчанням, можна повторити обчислення з більшою точністю та меншим допустимим відхиленням. Використання такої перевірки особливо рекомендовано для задач з вимогою цілочисельності змінних.
	Допустимое отклонение
	Линейная модель	Використовується для пошуку рішень лінійної задачі оптимізації або лінійної апроксимації нелінійної задачі. У випадку нелінійної задачі прапорець Линейная модельповинен бути не активований, інакше є можливість отримання невірного результату.
	Показывать результаты итераций	Для призупинення пошуку рішення і перегляду окремих ітерацій.
	Автоматическое масштабирование	Опція призначена для включення автоматичної нормалізації вхідних і вихідних значень, що якісно відрізняються за величиною. Наприклад, під час максимізації прибутку у відсотках по відношенню до великих сум капіталовкладень.
	Оценки	Існує для вибору методу екстраполяції.
	Разности	Група призначена для вибору методу чисельного диференціювання.
	Метод поиска	Існує для вибору алгоритму оптимізації.

Збереження (завантаження) різних даних для пошуку рішення здійснюється за допомогою кнопок Сохранить модель і Загрузить модель, відповідно, вікна Параметры поиска решения.

Побудова математичної моделі задачі оптимізації. Робота по вирішенню певної оптимізаційної задачі починається з побудови математичної моделі, для чого потрібно відповісти на такі питання:

v Які змінні моделі (для визначення яких величин будується модель)?

v Яке цільове значення функції (мета, для досягнення якої з множини всіх допустимих значень змінних обираються оптимальні)?

v Яким обмеженням повинні задовольняти невідомі?

При конструюванні математичної моделі формулювання обмежень є найвідповідальнішою частиною. У деяких випадках обмеження є очевидними, наприклад, обмеження на кількість сировини. Інші обмеження можуть бути вказані невірно. Наприклад:

v В моделі з кількома періодами часу величина матеріального ресурсу на початок наступного періоду повинна дорівнювати величині цього ресурсу на кінець попереднього періоду.

v В моделі поставок величина запасу на початок періоду плюс кількість отриманого повинна дорівнювати величині запасу на кінець періоду плюс кількість відправленого.

v Більшість величин в моделі за своїм фізичним сенсом не можуть бути від’ємними.

При максимізації цільової функції область допустимих значень повинна бути обмежена згори, при мінімізації – знизу.

Більшу частину задач оптимізації являють собою задачі лінійного програмування, у яких критерій оптимізації та обмеження – лінійні функції. В цьому випадку для вирішення задачі слід встановити прапорець Линейная модель у вікні Параметры поиска решения, що забезпечить використання симплекс-методу, інакше будуть використовуватись більш загальні (більш повільні) методи.

Пошук рішення може працювати також з нелінійними залежностями та обмеженнями. Це задачі нелінійного програмування, наприклад, вирішення системи нелінійних рівнянь. Вирішуючи задачі з нелінійними залежностями, слід:

v ввести початкові значення змінних для подальшого пошуку, наприклад, виконавши графічне представлення рішення, зробивши наближені припущення про рішення;

v у вікні Параметры поиска решении зняти прапорець Линейная модель.

Можна отримати звіт про пошук рішення. Звіти бувають трьох типів:

v Отчет по результатам вміщує кінцеві значення параметрів задачі цільової функції та обмежень;

v Отчет по устойчивости показує результати малих змін параметрів пошуку рішення;

v Отчет по пределам показує зміни рішення при виконанні почергової максимізації і мінімізації кожної змінної за умови незмінюваності інших змінних.

Дата добавления: 2014-11-29