Опис звітів про рішення задачі

Звіт по результатах (рис. 6) – таблиця Целевая ячейка виводить відомості про цільову функцію; таблиця Изменяемые ячейки показує значення змінних, отримані в результаті вирішення задачі; таблиця Ограничения відображає результати оптимального вирішення для обмежень і для граничних умов. В полі Формула наведені залежності, що були введені у вікно Поиск решения, в поле Разница – величини використаного матеріалу. Якщо матеріал використаний повністю, то в полі Статус виводиться связанное, за неповного використання матеріалу в цьому полі виводиться не связан. Для граничних умов замість величини невикористаного продукту показана різниця між значенням змінної і заданої для неї граничною умовою.

Рис. 6.

Звіт по стійкості (рис. 7) – у таблиці Изменяемые ячейки наводиться результат вирішення задачі. У таблиці Ограничения показуються значення обмежень, для яких зберігається оптимальний набір змінних, що входять у оптимальне рішення.

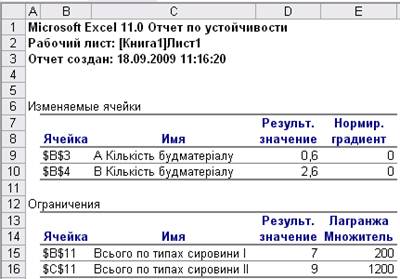
Рис. 7.

Звіт по лімітах (рис. 8) – у звіті показано, у яких лімітах може змінюватися кількість матеріалів в оптимальному рішенні; наводяться значення змінних у оптимальному рішенні, а також нижні і верхні границі зміни значень змінних; вказані значення цільової функції за умови випуску даного типу продукції на верхній та нижній границях.

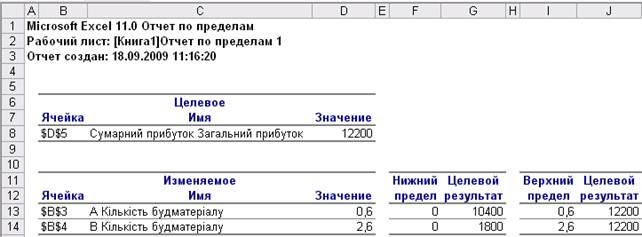
Рис. 8.

Приклад №2. Визначення складу добрив.

Для випуску добрив типів 1 і 2 використовуються хімічні речовини А, В, С і D, вимоги до змісту яких у добривах наведені в табл. 5. Для першого типу добрив: не більше 70% речовини А і не більше 40% речовини В; для другого типу добрив: від 30% до 50% речовини В, не менше 25% С і не більше 65% D.

Характеристики і запаси мінералів, що використовуються для виробництва хімічних речовин А, В, С і D, наведені в табл. 6.

Таблиця 5

Таблиця 6

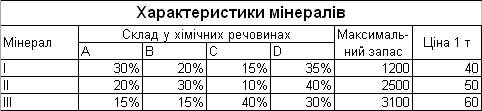
Ціна 1 т добрива типу 1 дорівнює 320 у.о., ціна 1 т добрива типу 2 – 350 у.о. Необхідно максимізувати прибуток від продажу добрив типів 1 і 2.

Для вирішення даної задачі будемо використовувати програму MS Excel, процедуру Поиск решения. Запишемо умови задачі у робочій книзі ( рис. 9).

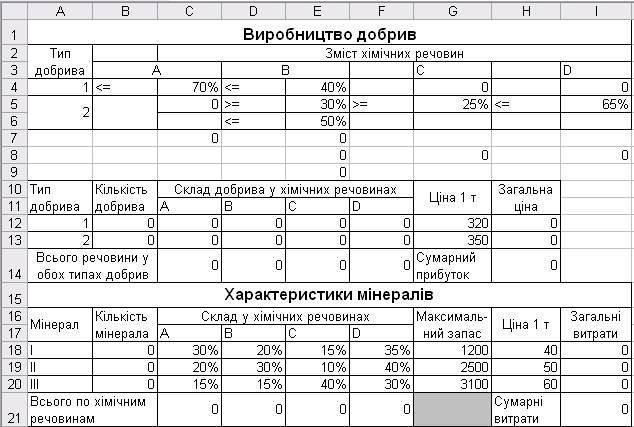
Рис. 9.

Для математичного запису обмежень на зміст хімічних речовин у добривах використовуються допоміжні клітини: 70% речовини А у добриві типу 1 записано у клітині С7 (=C4*B12), обмеження на зміст речовини В - Е7 (=B12*E4), Е8 (=B13*E5), Е9 (=B13*E6), на зміст речовини С - G8 (=G5*B13), на зміст D - І8 (=I5*B13).

Кількість добрива визначається як сумарний склад добрива у хімічних речовинах, наприклад для добрива типу 1 – у клітині В12 (=СУММ(C12:F12)).

Загальна ціна всього об’єму добрив типів 1 і 2 у клітинах Н12 і Н13 визначається за допомогою формули масиву {=B12:B13*G12:G13}. Загальна кількість речовини А у обох типах добрив у клітині С14 знаходиться за формулою: =СУММ(C12:C13), аналогічно для інших речовин. Загальна кількість речовини А у трьох типах мінералів у клітині С21 знаходиться за формулою масиву {=СУММ($B$18:$B$20*C18:C20)}, для інших речовин – формула копіюється. Загальні витрати у масиві клітин I18:I20 визначаються за формулою масиву {=B18:B20*H18:H20}.

Сумарний прибуток у клітині Н14 визначається як різниця сумарної загальної ціни і сумарних витрат: =СУММ(H12:H13)-I21.

Формулювання математичної моделі задачі:

v змінні для вирішення задачі: кількість хімічних речовин А, В, С і D у добривах типів 1 і 2 (С12:F13) та кількість мінералів I, II і III (В18:В20);

v визначення цільової функції (критерію оптимізації): серед усіх припустимих значень змінних знайти таку кількість хімічних речовин і мінералів, що максимізують сумарний прибуток від виробництва (Н14);

v обмеження на змінні: об’єми виробництва хімічних речовин та мінералів не можуть бути від’ємними (С12:F13≥0, В18:В20≥0), а також кількість мінералів не може перевищувати максимально можливих запасів (В18:В20≤G18:G20) та кількість хімічних речовин А, В, С і D у добривах не може бути більше, ніж кількість речовин у мінералах (С14:F14≤C21:F21);

v обмеження на відсотковий зміст хімічних речовин у добривах згідно з умовами задачі - обмеження на зміст речовини А: у першому типі добрив С12≤С7, на зміст речовини В: у першому типі добрив D12≤E7, у другому типі добрив D13≤E9 і D13≥E8, на зміст речовини С: у другому типі добрив E13≥G8, на зміст речовини D:, у другому типі добрив F13≤I8.

Для вирішення даної задачі будемо використовувати програму Excel, інструмент Поиск решения. Обираємо опцію Сервис, Поиск решения. У вікні Поиск решения встановлюємо максимальне значення у цільовій клітині Н14, вказуємо для зміни клітини С12:F13 та В18:В20 і додаємо обмеження.

У вікні Параметры встановлюємо параметри пошуку рішення (метод оцінки, метод чисельного диференціювання та алгоритм оптимізації). У вікні Результаты поиска решения задаємо виведення всіх типів звітів.

Результати вирішення задачі показані на рис. 10.

Рис. 10.

Завдання до розділу «Лінійна оптимізація»

1. Підприємство випускає продукцію чотирьох типів П₁-П₄, для виготовлення якої використовуються ресурси трьох видів: трудові, сировина і обладнання. Норми витрат кожного виду ресурсу на виготовлення одиниці кожного типу продукції наведені у табл. 7.

Таблиця 7

Ресурс	Тип продукції	Об’єм ресурсу
П1	П2	П3	П4
Трудовий
Сировина
Обладнання

Прибуток, отриманий від реалізації одиниці продукції, дорівнює: для продукції П₁ – 60 у.о., для П₂ – 70 у.о., для П₃ – 120 у.о., для П₄ – 130 у.о. Визначити оптимальний план виробництва кожного типу продукції, що максимізує прибуток підприємства.

2. Магазин реалізує три типи продукції П₁, П₂, П₃. Для цього використовується два обмежених ресурси – корисна площа приміщень, яка з врахуванням коефіцієнта оберненості складає 450 м², і робочий час працівників магазину – 600 людино-годин. Товарообіг повинен бути не менше 240 000 у.о. Необхідно розробити план товарообігу, що приносить максимум прибутку.

Витрати ресурсів на реалізацію та отриманий прибуток представлені у табл.. 8.

Таблиця 8

Ресурси	Витрати ресурсів на реалізацію, тис. у.о.	Об’єм ресурсів
П1	П2	П3
Корисна площа, м^2	1,5
Робочий час, людино-годин			1,5
Прибуток, тис. у.о.

3. Двом навантажувачам різної потужності не більше, ніж за 24 години потрібно завантажити на першому майданчику 230 тон, на другому - 168 тон. Перший навантажувач на першому майданчику може вантажити 10 тон на годину, на другому – 12 тон на годину. Другий навантажувач на кожному майданчику може вантажити по 13 тон на годину. Вартість робіт, пов’язаних із навантаженням однієї тони першим навантажувачем на першому майданчику – 8 у.о., на другому – 7 у.о., другим навантажувачем на першому майданчику – 12 у.о., на другому – 13 у.о. Потрібно скласти план роботи, тобто знайти, який об’єм робіт повинен виконати кожен навантажувач на кожному майданчику, щоб вартість всіх робіт при навантаженні була мінімальною. Слід врахувати, що по технічних причинах перший навантажувач на другому майданчику повинен працювати не більше 16 годин.

4. Цех випускає два види продукції П₁ та П₂,, використовуючи два типи напівфабрикатів. Продукція використовується при комплектуванні виробів, при цьому на кожну одиницю продукції першого виду потрібно не більше двох одиниць продукції другого виду. Норми витрат напівфабрикатів кожного типу на одиницю продукції, загальні об’єми напівфабрикатів та прибуток від реалізації одиниці продукції кожного виду наведені у табл. 9. Скласти план виробництва, що приносить максимум прибутку.

Таблиця 9

Напівфабрикати	Витрати ресурсів на реалізацію, тис. у.о.	Об’єм напівфабрикатів
П1	П2
Прибуток, у.о.

5. Спеціалізація і технологічні можливості дозволяють підприємству випускати чотири види продукції П₁, П₂, П₃ і П₄ Збут будь-якої кількості продукції забезпечений. Для виготовлення продукції використовуються трудові ресурси, напівфабрикати і верстатне устаткування. Об’єм ресурсів, витрати кожного ресурсу на одиницю продукції і прибуток, отриманий за одиницю продукції, наведені у табл. 10. Скласти план виробництва, що приносить максимум прибутку.

Таблиця 10

Ресурси	Витрати ресурсів на одиницю продукції	Об’єм ресурсів
П1	П2	П3	П4
Трудові ресурси, людино-годин
Напівфабрикати, кг
Верстатне устаткування, верстато-годин
Прибуток на одиницю продукції, у.о.

6. Підприємство випускає два види продукції П₁ і П₂ Збут будь-якої кількості продукції забезпечений. Для виготовлення продукції використовуються трудові ресурси, сировина і устаткування. Об’єм ресурсів, витрати кожного ресурсу на одиницю продукції і прибуток, отриманий за одиницю продукції, наведені у табл. 11. Скласти план виробництва, що приносить максимум прибутку.

Таблиця 11

Ресурси	Витрати ресурсів на одиницю продукції	Об’єм ресурсів
П1	П2
Трудові ресурси
Сировина
Устаткування
Прибуток на одиницю продукції

7. Необхідно скласти дієту, що складається з двох продуктів А і В. Денне споживання цих продуктів повинно давати не більше 14 одиниць жиру, але не менше, ніж 300 калорій. В одному кілограмі продукту А міститься 15 одиниць жиру і 150 калорій, а в одному кілограмі продукту В – 4 одиниці жиру і 200 калорій. При цьому ціна одного кілограму продукту А дорівнює 15 у.о., а ціна одного кілограму продукту В – 25 у.о. Яку кількість продуктів на день потрібно споживати для дотримання дієти, щоб вкладені кошти були мінімальними.

8. Для випуску чотирьох видів продукції П₁, П₂, П₃ і П₄ на підприємстві використовують три типи сировини С₁, С₂, і С₃. Об’єм сировини, норми витрати сировини на одиницю продукції і прибуток, отриманий за одиницю продукції, наведені у табл. 12. Скласти план виробництва, що приносить максимум прибутку.

Таблиця 12

Сировина	Витрати сировини на одиницю продукції	Запаси сировини
П1	П2	П3	П4
С1
С2
С3
Прибуток на одиницю продукції

9. Фабрика випускає три види тканин, при цьому добове планове завдання становить не менше 90 м тканин першого виду, 70 м – другого та 60 м – третього. Добові ресурси такі: 780 одиниць виробничого обладнання, 850 одиниць сировини і 790 одиниць електроенергії, витрати яких на один метр тканин показані у табл. 13.

Таблиця 13

Ресурси	Витрати сировини на один метр тканин
Т1	Т2	Т3
Устаткування
Сировина
Електроенергія

Ціна одного метра тканини першого виду дорівнює 80 у.о., другого – 70 у.о., третього – 60 у.о. Визначити, скільки метрів тканини кожного виду слід випустити, щоб загальна вартість продукції була максимальною.

10. Фірма випускає два види деревно-стружкових плит – звичайні і поліпшені. При цьому виконуються дві основні операції – пресування та обробка. Яку кількість плит кожного виду можна виготовити на протязі місяця, щоб забезпечити максимальний прибуток при заданих (табл. 14) обмеженнях на ресурси (матеріал, час, витрати).

Таблиця 14

Ресурси	Витрати ресурсів на партію з 100 плит	Об’єм ресурсів
звичайних	поліпшених
Матеріал (кг)
Час на пресування (години)
Час на обробку (години)
Витрати (у.о.)
Прибуток партію з 100 плит (у.о.)

11. Фірма виробляє два види продукції: столи та стільці. Для виготовлення одного стільця потрібно використати 3 кг деревини та витратити дві години робочого часу, а для виготовлення одного стола – 7 кг і 8 годин часу. Кожен стілець приносить прибуток 1 у.о., а стіл – 3 у.о. Скільки стільців і столів повинна виготовити фірма, якщо вона має в своєму розпорядженні 420 кг деревини і 400 годин робочого часу на тиждень, для отримання максимального прибутку?

12. Для виготовлення виробів типу А і В завод може виділити не більше, ніж 80 кг металу. Деталей типу А завод може виготовити за добу не більше 30 шт., типу В – не більше 40 шт. Ціна одного виробу типу А становить 3 у.о., типу В – 5 у.о. Для виготовлення однієї деталі типу А використовується 2 кг металу, типу В – 1 кг. Скласти план виробництва, що приносить максимум прибутку.

Транспортна задача

У загальному вигляді транспортну задачу можна сформулювати таким чином: в m пунктах відправлення А₁ ,…, А_n знаходиться однорідний вантаж, кількість якого дорівнює а₁ ,…, а_n одиниць. Вантаж потрібно доставити споживачам В₁ ,…, В_n, попит яких становить b₁ ,…, b_n. Вартість перевезення одиниці вантажу з i -го (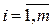) пункту відправлення до j -го () пункту призначення дорівнює 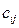. Необхідно скласти план перевезень, що повністю задовольнить попит споживачів у вантажі, при цьому сумарні транспортні витрати мінімальні.

Модель транспортної задачі називають закритою (збалансованою), якщо сумарний об’єм вантажу, що є у постачальників, дорівнює сумарному попиту споживачів, інакше модель задачі є відкритою (незбалансованою).

Приклад транспортної задачі. Виробництво продукції здійснюється на чотирьох підприємствах, а потім доставляється у п’ять пунктів споживання. Підприємства можуть випускати на день 235, 175, 185 і 175 одиниць продукції. Пункти споживання готові приймати щодня 125, 160, 60, 250 і 175 одиниць продукції. Зберігання на підприємстві одиниці продукції обходиться у 2 у.о. на день, штраф за недопостачання – 3,5 у.о. на день за одиницю продукції. Вартість перевезення одиниці продукції (в у.о.) з підприємств у пункти споживання наведена у табл. 15.

Таблиця 15

Підприємства	Пункти споживання
	3,2		2,35		3,65
		2,85	2,5	3,9	3,55
	3,75	2,5	2,4	3,5	3,4
			2,1	4,1	3,4

Необхідно мінімізувати загальні транспортні витрати з перевезення продукції.

Для вирішення даної задачі будемо використовувати програму MS Excel, процедуру Поиск решения. Запишемо умови задачі у робочій книзі ( рис. 11).

Рис. 11.

Недопостачання визначається як різниця між обсягом споживання і сумарною кількістю перевезень у пункт споживання: {=B9:F9-B8:F8}. Залишки на підприємстві знаходяться як різниця між обсягом виробництва і сумарними перевезеннями з підприємства: {=H4:H7-G4:G7}.

Сумарна кількість перевезень у пункт 1 в клітині В8 знаходиться за формулою =СУММ(B4:B7), ця формула копіюється на клітини С8:F8. Сумарна кількість перевезень з підприємства 1 в клітині G4 визначається за формулою =СУММ(B4:F4), потім ця формула копіюється на клітини G5:G7.

У клітині Н9 визначається, чи збалансована задача (=ЕСЛИ(ОКРУГЛ(G9;0)=ОКРУГЛ(H8;0);"Задача збалансована";"Задача не-збалансована")) шляхом порівняння загального обсягу споживання у клітині G9 (=СУММ(B9:F9)) і загального обсягу виробництва у клітині Н8 (=СУММ(H4:H7)).

Знаходимо вартість зберігання залишків у клітині J4 ({=СУММ(I4:I7;B8:F8-B9:F9)*2}) і штраф за недопостачання ({=СУММ(B9:F9-B8:F8)*3,5}) у клітині J7.

Вартість перевезень у пункт споживання 1 у клітині В18 знаходиться за формулою масиву {=СУММ(B4:B7*B14:B17)}, потім ця формула копіюється на клітини С18:F18. Загальна вартість перевезень визначається за формулою: =СУММ(B18:F18).

Формулювання математичної моделі задачі:

v змінні для вирішення задачі: кількість перевезень з підприємств у пункти споживання (В4:F7);

v визначення цільової функції (критерію оптимізації): серед усіх припустимих значень змінних знайти таку кількість перевезень з підприємств у пункти споживання, що мінімізують загальні транспортні витрати з перевезення продукції (В19);

v обмеження на змінні: об’єми перевезень не можуть бути від’ємними (В4:F7≥0);

v оскільки модель збалансована, то вся продукція повинна бути вивезена з підприємств, а потреби всіх пунктів споживання повинні бути повністю задоволені, у загальному вигляді: сумарна кількість перевезень у кожен пункт споживання з усіх підприємств повинна бути не менше обсягу споживання (В8:F8≥B9:F9) та сумарна кількість перевезень з кожного підприємства не може бути більше, ніж обсяг виробництва (G4:G7≤H4:H7).

Для вирішення даної задачі будемо використовувати програму Excel, інструмент Поиск решения. Обираємо опцію Сервис, Поиск решения. У вікні Поиск решения встановлюємо мінімальне значення у цільовій клітині В19, вказуємо для зміни клітини В4:F7 і додаємо обмеження.

Результати вирішення задачі показані на рис. 12. Об’єми залишків на підприємстві і недопостачання є нульовими.

Рис. 12.

Завдання до розділу «Транспортна задача»

Виробництво продукції здійснюється на кількох підприємствах, а потім доставляється у пункти споживання. Об’єм виробництва на підприємствах, попит на продукцію у пунктах споживання і вартість перевезення одиниці продукції з кожного підприємства у кожен пункт споживання наведена у таблицях 16 – 27. Зберігання на підприємстві одиниці продукції обходиться у 1,6 у.о. на день, штраф за недопостачання – 3,4 у.о. на день за одиницю продукції. Скласти план перевезення з доставки продукції у пункти споживання, що мінімізує транспортні витрати.

1. Таблиця 16

Підприємства	Вартість перевезення одиниці продукції, у.о.	Об’єм виробництва
Пункти споживання
		1,8
		5,1
	3,5			3,1
	2,2	4,9	1,3
			8,95
Об’єм споживання

2. Таблиця 17

Підприємства	Вартість перевезення одиниці продукції, у.о.	Об’єм виробництва
Пункти споживання
	2,3
		1,3		2,5
	4,9
		2,1	1,2
Об’єм споживання

3. Таблиця 18

Підприємства	Вартість перевезення одиниці продукції, у.о.	Об’єм виробництва
Пункти споживання
			4,1
		2,5
				4,2
	5,1
Об’єм споживання

4. Таблиця 19

Підприємства	Вартість перевезення одиниці продукції, у.о.	Об’єм виробництва
Пункти споживання
	1,7
	5,2	2,6	9,8
			2,5
Об’єм споживання

5. Таблиця 20

Підприємства	Вартість перевезення одиниці продукції, у.о.	Об’єм виробництва
Пункти споживання
			4,8
	5,5
			8,2
	1,8
Об’єм споживання

6. Таблиця 21

Підприємства	Вартість перевезення одиниці продукції, у.о.	Об’єм виробництва
Пункти споживання
	6,2		4,2
			5,1
		2,75
Об’єм споживання

7. Таблиця 22

Підприємства	Вартість перевезення одиниці продукції, у.о.	Об’єм виробництва
Пункти споживання
Об’єм споживання

8. Таблиця 23

Підприємства	Вартість перевезення одиниці продукції, у.о.	Об’єм виробництва
Пункти споживання
				7,4
		2,2
	2,5
Об’єм споживання

9. Таблиця 24

Підприємства	Вартість перевезення одиниці продукції, у.о.	Об’єм виробництва
Пункти споживання
	6,3	8,6
	2,5
Об’єм споживання

10. Таблиця 25

Підприємства	Вартість перевезення одиниці продукції, у.о.	Об’єм виробництва
Пункти споживання
	7,3
	4,8
Об’єм споживання

11. Таблиця 26

Підприємства	Вартість перевезення одиниці продукції, у.о.	Об’єм виробництва
Пункти споживання
	6,3
		5,5
Об’єм споживання

12. Таблиця 27

Підприємства	Вартість перевезення одиниці продукції, у.о.	Об’єм виробництва
Пункти споживання
	4,2
				7,3
Об’єм споживання

Дата добавления: 2014-11-29