Вправи до розділу 4. Вправа 4.1. Користуючись співвідношенням (4.10) і методом ранжування побудувати порядкові функції корисності для множини елементів

Вправа 4.1. Користуючись співвідношенням (4.10) і методом ранжування побудувати порядкові функції корисності для множини елементів .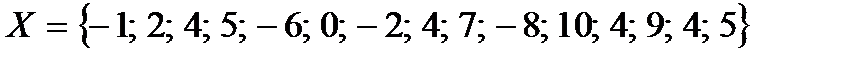

Вправа 4.2. В результаті застосування методу половинного поділу за корисністю отримано такі результати:

Прибуток	Корисність

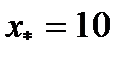
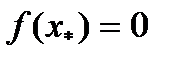
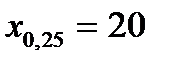
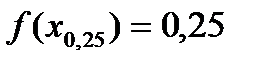
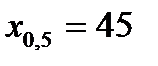
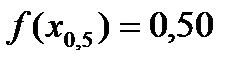
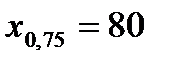
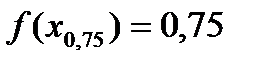
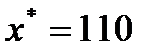
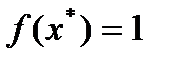
Підібрати функцію і виконати апроксимацію переваг ОПР щодо прибутку на множині значень [10; 110].

Вправа 4.3. Лотерея з ймовірністю 0,5 призводить до результату 35 або 45 гр.од., тобто 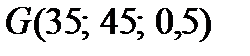. Обчислити математичне сподівання виграшу, детермінований еквівалент і премію за ризик, якщо функція корисності має вигляд 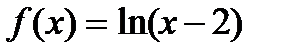. Вказати тип ставлення ОПР до ризику за даною функцією корисності.

Вправа 4.4. Інвестор має можливість вкласти кошти в один із інвестиційних проектів (А або В), ймовірні прибутки за якими подано у таблиці:

Ситуація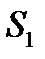
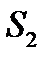
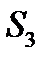
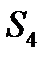
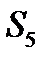
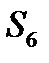
Ймовірність	0,05	0,05	0,2	0,4	0,2	0,1
Прибуток за проектом А, тис.грн.
Прибуток за проектом В, тис.грн.

Визначити, який із двох інвестиційних проектів слід вважати привабливішим для інвестора, якщо його функція корисності має вигляд .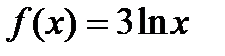

Вправа 4.5. ОПР має справу з лотереєю 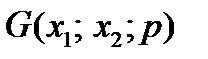. Знайти математичне сподівання виграшу і детермінований еквівалент лотереї, якщо функція корисності має вигляд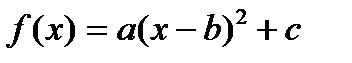

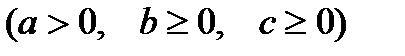, для ; ; .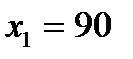

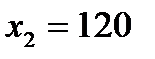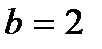Вправа 4.6. ОПР має функцію корисності 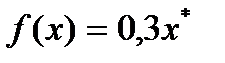. Якій із лотерей 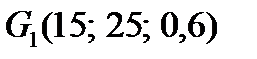і 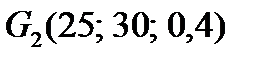ОПР віддасть перевагу?

Вправа 4.7. Особа з функцією корисності 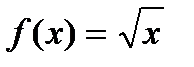обирає місце роботи, виходячи із двох альтернатив. Для місця роботи А заробітна плата може складати 1500 грн. з ймовірністю 0,5 або 3100 грн. з тією ж ймовірністю. У місці роботи В їй пропонується гарантована заробітна плата у розмірі 2100 грн. Яке місце роботи слід вважати кращим?

Вправа 4.8. Особа має три альтернативні варіанти щодо вибору місця роботи:

А – зі стабільним доходом у розмірі 695 гр.од.;

В – дохід 615 гр.од. з ймовірністю 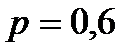і дохід 815 гр.од. з ймовірністю ;

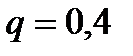С – дохід 485 гр.од. з ймовірністю 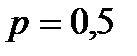і дохід 905 гр.од. з тією ж ймовірністю.

Визначити, яке місце роботи обрати собі, якщо її функція корисності є зрізаним на проміжку [450; 1450], нормальним законом розподілу з математичним сподіванням і дисперсією .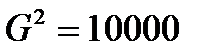

Вправа 4.9. Капітал страхової компанії під інвестиції складає 10 млн.грн. Вважаючи, що функція корисності керівництва компанії має вигляд 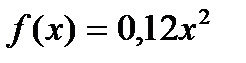, необхідно вирішити питання поро використання інвестиційних коштів протягом року за двома можливими альтернативними варіантами:

а) придбати державні цінні папери з річною нормою прибутку 8%;

б) придбати ризикові акції корпорацій під 20% річних, причому ймовірність отримання обіцяного прибутку складає 0,65 (у випадку невдачі страхова компанія повертає первинний капітал). Який вибір доцільно зробити керівництву страхової компанії?

Вправа 4.10. Знайти оптимальний бюджетний план споживання для задачі:

,

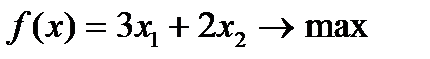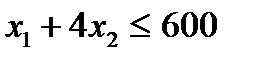(бюджетне обмеження),

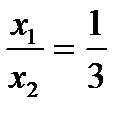(структура споживання),

.

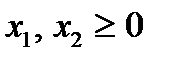Дата добавления: 2014-11-29