Функція корисності і моделювання поведінки споживачів

При обґрунтуванні обсягів випуску продукції і надання послуг важливим є дослідження обмежень на виробництво, зміст якого зводиться до моделювання поведінки споживачів в залежності від цін на товари (послуги) і доходи.

Множину різноманітних за номенклатурою і обсягом наборів із 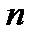товарів, які можна запропонувати споживачеві прийнято називати простором товарів.

Таблиця 4.1

Взаємозв’язок між абсолютною і граничною корисністю

Функція корисності	Функція граничної корисності
Лінійна: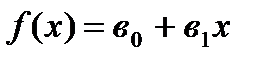
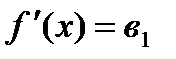
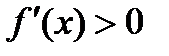
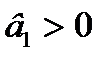
Квадратична: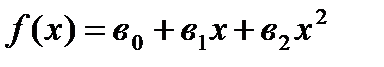
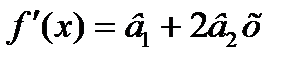
а)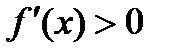
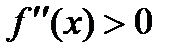
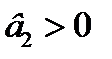
б)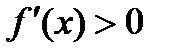
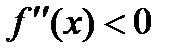
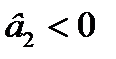
Кубічна: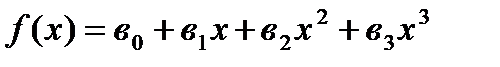
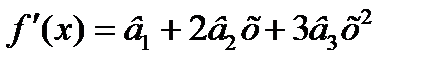
а)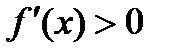
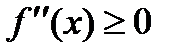
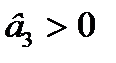
б)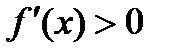

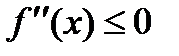
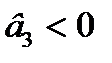
За умови, що ціна 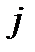-го виду товару складає 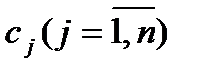, а капітал (дохід) споживача складає 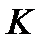, формується набір товарів, який може придбати споживач – бюджетна множина:

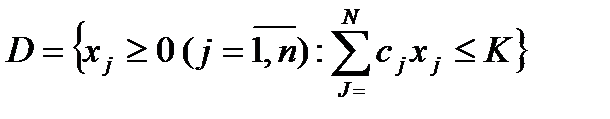. (4.14)

Нехай у просторі товарів задана функція корисності споживача 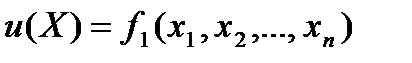. Так як споживач намагається отримати найбільшу корисність за обмеженого доходу, то його рішення щодо купівлі того чи іншого набору товарів можна інтерпретувати як вибір точки на бюджетній множині, яка максимізує функцію корисності:

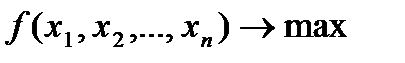, (4.15)

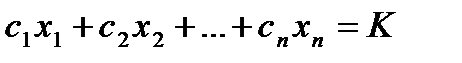, (4.16)

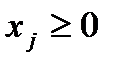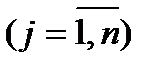, . (4.17)

Рівняння (4.16) називають бюджетною лінією.

Задача (4.15) – (4.17) є задачею на умовний екстремум. Якщо скористатися функцією Лагранжа

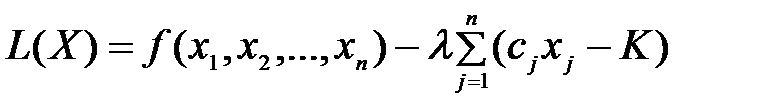, (4.18)

то можна отримати необхідні умови існування локального екстремуму:

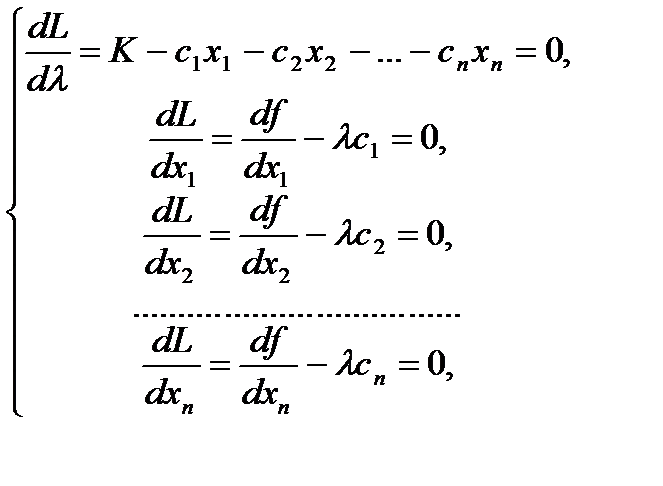(4.19)

або

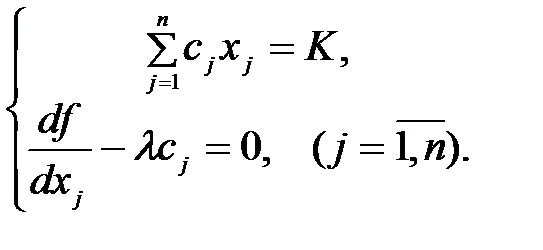(4.20)

Розв’язавши систему рівнянь (4.20), знаходять набір товарів 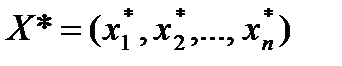, який забезпечує максимізацію функції корисності споживача за фіксованого доходу 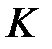і встановлених цін на товари.

Із (4.20) можна зробити висновок:

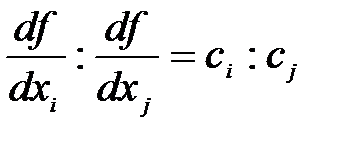, (4.21)

тобто у точці 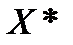відношення граничної корисності дорівнює відношенню цін. Нагадаємо, що гранична корисність товару

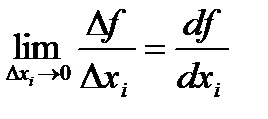
показує, на яку величину зростає корисність, якщо кількість товару зростає в малому обсязі.

Гіперповерхню розмірності 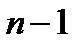, на якій корисність є постійною величиною, тобто 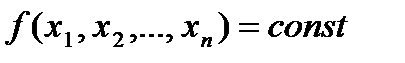, називають поверхнею байдужості.

Так як для різних значень наборів товарів, які лежать на конкретній поверхні байдужості, функція корисності є константою, то можна говорити про взаємозамінність товарів – можливість заміни одного товару певним обсягом іншого товару.

Для поверхні байдужості виконується умова

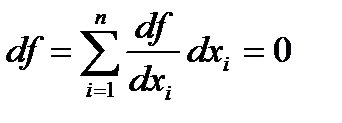, (4.22)

яка вказує, що дотична до неї перпендикулярна градієнтові корисності. Якщо прийняти, що 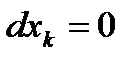для всіх 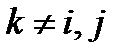, то (4.22) набере вигляду:

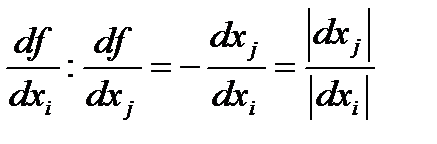. (4.23)

Відношення граничної корисності одного виду товару до граничної корисності другого називають граничною нормою заміщення. Вона показує скільки одиниць 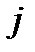-го товару потрібно для того, щоб замінити малий обсяг 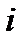-го товару, який вибув. Величини 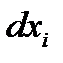і 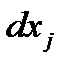у (4.23) повинні мати різні знаки, оскільки скорочення обсягів споживання одного товару супроводжується зростанням обсягів споживання іншого.

У процесі побудови функції корисності споживача потрібно орієнтуватися на гіпотези теорії споживання, які ставлять такі вимоги до властивостей функції:

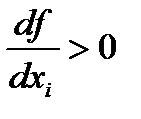▪ - зростання споживання блага призводить до зростання корисності;

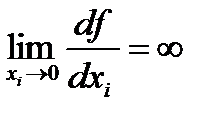▪ - невеликий приріст блага за його початкової відсутності різко збільшує корисність;

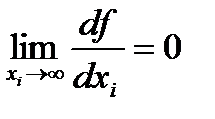▪ - якщо існує достатньо великий обсяг блага, то його подальше зростання не призводить до зростання корисності;

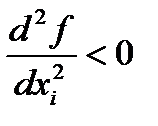▪ - зростання споживчого блага веде до того, що швидкість зростання корисності спадає.

Найпростіша модель споживання для двох товарів має такий вигляд:

функція корисності: ,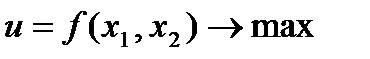

бюджетна лінія: ,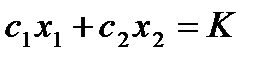

.

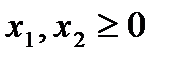До моделі також можуть бути включені обмеження на нижній і верхній рівень споживання блага:

,

.

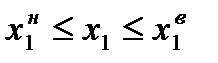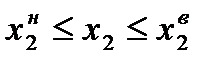Оптимальний план споживання знаходиться у точці дотику бюджетної лінії до кривої байдужості

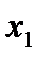
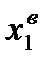
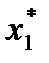
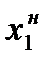
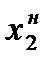
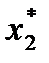
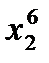
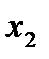
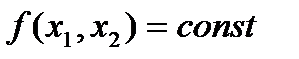
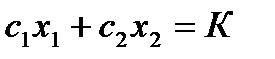
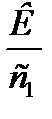
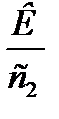
Рис.4.1. Графічна інтерпретація моделі споживання

Розглянемо таку задачу споживання:

,

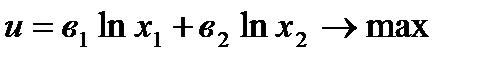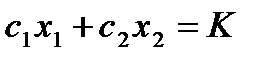, (4.25)

.

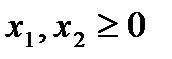Для розв’язання задачі (4.25) будуємо функцію Лагранжа:

.

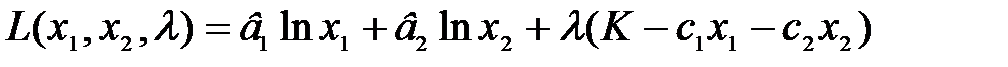Тоді згідно (4.20) необхідні умови існування екстремуму є такими:

.

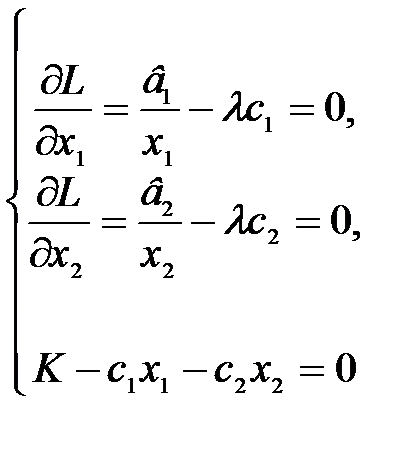На основі перших двох рівнянь отримуємо:

.

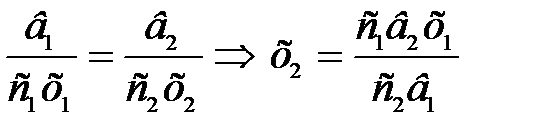Підставляємо останній вираз у рівняння бюджетної лінії:

.

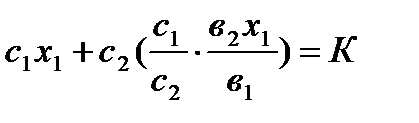Далі отримуємо оптимальний план задачі (4.25):

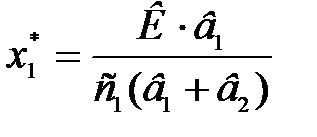, (4.25)

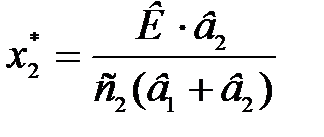. (4.26)

►Приклад 4.1. Знайти оптимальний план такої задачі споживання:

,

,

.

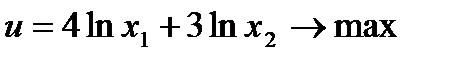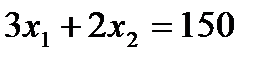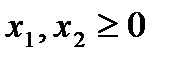Вище за допомогою методу Лагранжа було отримано аналітичні вирази для знаходження оптимального плану задачі, представленої у загальному вигляді. Тому скористаємося (4.26) і (4.27):

;

. ◄

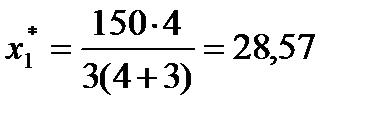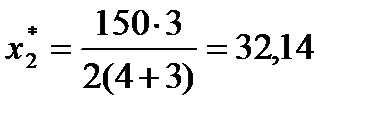Дата добавления: 2014-11-29