Аналіз конфліктних ситуацій

РОЗДІЛ 5. ОБГРУНТУВАННЯ РІШЕНЬ В УМОВАХ КОНФЛІКТНОСТІ, НЕВИЗНАЧЕНОСТІ ЗОВНІШНЬОГО СЕРЕДОВИЩА І БАГАТОКРИТЕРІАЛЬНОСТІ ВИБОРУ

В господарській діяльності нерідко зустрічаються конфліктні ситуації – ситуації, в яких два (або декілька) учасників ринку мають суперечливі цілі. Конфлікти мають різноманітний характер (взаємовідносини між банками і клієнтами, виробниками продукції і споживачами тощо), вважаються природним станом для суб’єктів господарювання і породжуються прагненням отримати максимальний зиск від підприємницької діяльності. Потрібно зауважити, що кожному учаснику конфліктної ситуації потрібно рахуватися не тільки із власними цілями, але й цілями суперника (інших учасників).

Наявність конфлікту вважається однією із передумов виникнення ризиків, а отже вимагає застосування необхідного математичного апарату для кількісного аналізу відповідних ситуацій. Математичну теорію конфліктних ситуацій, яку започаткував Дж.Нейман¹, називають теорією ігор.

Математичну модель конфліктної ситуації називають грою, сторони, які приймають участь у грі, – гравцями, а результат конфліктної ситуації – виграшем. Для кожної формалізованої гри задається система умов (правила гри), яка визначає можливі варіанти дій гравців, обсяг інформації кожної сторони про поведінку іншої, а також результат, до якого призводить сукупність дій.

Вибір і реалізація однієї із передбачених правилами дій називається ходом, а сукупність правил для вибору варіанта дій при кожному ході – стратегією гравця. Мета теорії ігор – визначення оптимальних стратегій для кожного із гравців. Оптимальною для гравця називається стратегія, яка забезпечує йому максимальний виграш (мінімальний програш). Варто зазначити, що в основі визначення оптимальної стратегії гравця лежить положення про ідеальну (розумну) поведінку його противника.

1. Нейман Дж., Моргенштерн.О. Теория игр и экономическое поведение. – М.: ИЛ, 1960. – 708 с.

Розрізняють парні ігри (участь у грі беруть два гравці) і множинні ігри.

У залежності від кількості стратегій, які знаходяться у розпорядженні гравців, ігри поділяють на скінченні і нескінченні, причому поняття нескінченної гри пов’язується не з тривалістю гри, а з кількістю стратегій.

Якщо гравцям дозволяється утворювати коаліції, які визначаються заздалегідь для координації своїх дій у процесі гри, то має місце кооперативна гра.

Якщо загальний капітал учасників гри не змінюється, а перерозподіляється залежно від результатів гри, то така гра називається грою з нульовою сумою. Парна гра з нульовою сумою називається антагоністичною грою або матричною грою з нульовою сумою. Це найпростіший і найкраще досліджений клас теорії ігор.

У парній грі з нульовою сумою беруть участь два гравці (А і В), які мають протилежні інтереси, причому вважають, що виграш одного гравця дорівнює програшу другого гравця, тобто сума виграшів обох гравців рівна нулеві. Перший гравець має у своєму розпорядженні 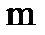стратегій (ходів), а другий володіє стратегіями. Якщо сформований набір стратегій для кожного гравця, то можна визначити функцію виграшів, яку задають у вигляді платіжної матриці 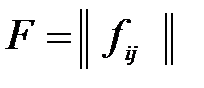розмірності 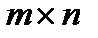, де елемент вказує на виграш гравця 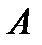(виграш гравця 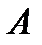дорівнює програшу гравця з протилежним знаком) за умови, що він використав свою і -ту стратегію, а гравець 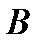- свою -ту стратегію.

Умови парної гри з нульовою сумою зазвичай записують у стандартній формі, загальний вигляд якої подано у табл.5.1.

Перед тим, як перейти до аналізу поведінки учасників конфліктної ситуації, яка вписується у схему матричної гри з нульовою сумою, необхідно зробити такі припущення:

▪ гравці однаково розумні і знають всі можливі стратегії суперника;

▪ кожен із гравців не знає, якою саме стратегією скористається його суперник (ходи робляться одночасно);

▪ у своїх діях гравці керуються лише кількісними характеристиками, представленими у платіжній матриці, і намагаються максимізувати свій фінансовий результат;

▪ гравці однаково оцінюють фінансові результати як для себе, так і для суперника.

Таблиця 5.1

Представлення умов парної гри з нульовою сумою

Стратегії гравців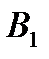

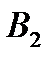
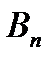
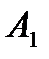
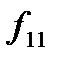
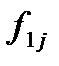
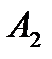
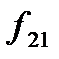
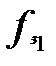
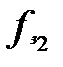
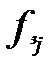
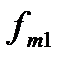
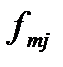
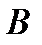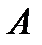У випадку, коли гравець вибере свою і -ту стратегію, то в найгіршому для себе випадку, враховуючи, що гравець на його хід відповість своїм найкращим ходом, він отримає виграш . Так як гравець може вибирати будь-яку зі своїх стратегій, то природно передбачити, що він вибере таку, за якої величина 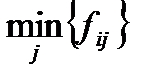стане найбільшою:

. (5.1)

Діючи за цим принципом (при найгіршій для себе поведінці гравця 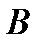) гравець отримає гарантований виграш 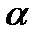. Величина 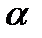називається нижньою ціною гри. Стратегія і _о, яка забезпечує гравцеві 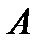отримання виграшу 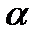, називається максмінною стратегією.

Гравець , міркуючи аналогічним чином, може забезпечити собі виграш :

. (5.2)

Величина має назву верхньої ціни гри, а стратегія гравця , що відповідає верхній ціні гри, називається мінімаксною. У теорії ігор доводиться, що

. (5.3)

Таким чином гравець , діючи згідно з максмінною стратегією, може бути впевнений у тому, що виграє не менше ніж 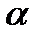, а гравець , користуючись мінімаксною стратегією, завадить йому отримати виграш, що перевищує .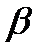

Якщо і _о та - це стратегії, при яких досягається рівність 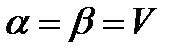, то вони називаються відповідно оптимальними чистими стратегіями гравця 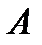та 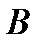, а величина - ціною гри. Сукупність чистих стратегій і _о та є розв’язком гри.

Матриця 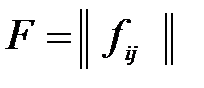, для якої виконується рівність 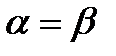, повинна мати елемент, який є мінімальним у своїй стрічці і максимальним у своєму стовпці. Такий елемент має назву сідлової точки.

Розв’язування задачі парної гри з нульовою сумою у чистих стратегіях покажемо на такому прикладі.

► Приклад 5.1. Фірма 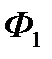планує випустити і збути на ринку чотири види продукції, а конкуруюча з нею фірма 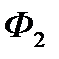може випускати і збувати на цьому ж ринку п’ять видів аналогічної продукції. Прибутки фірми 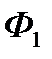в залежності від вибраної стратегії фірми задаються такою платіжною матрицею:

.

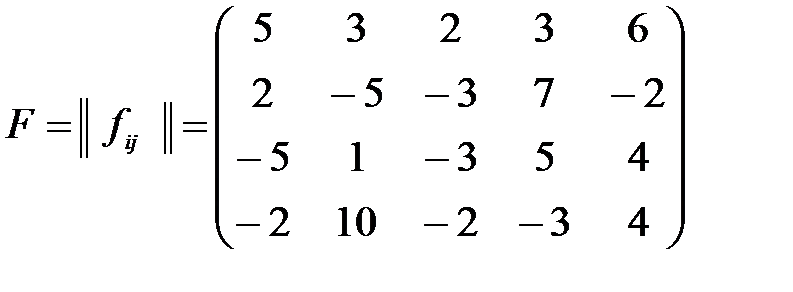Знайдемо оптимальні чисті стратегії фірми 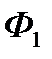і фірми 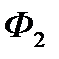вважаючи, що величина прибутку однієї фірми є недоотриманим прибутком другої фірми.

Результати розв’язання задачі представлені у табл.5.2.

Таблиця 5.2

Платіжна матриця гри

Стратегії гравців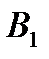
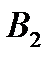
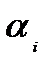
		-5	-3		-2	-5
	-5		-3			-5
	-2		-2	-3		-3

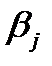
Останній стовпчик та рядок таблиці містять відповідно мінімальні значення кожного рядка та максимальні значення кожного стовпця платіжної матриці. Згідно принципу повної невизначеності та ідеальної поведінки фірм знаходимо:

;

.

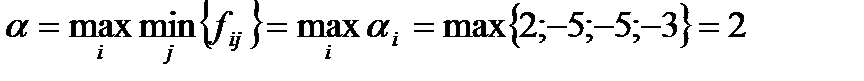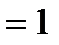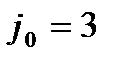Так як , то конфліктним сторонам можна вказати їх оптимальні стратегії: і _о - для фірми і - для фірми .

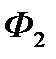Таким чином, фірма 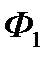матиме гарантований прибуток в розмірі 2 одиниці, а фірма 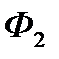не понесе збитки, що перевищать 2 одиниці. ◄

Якщо парна гра з нульовою сумою не має сідлової точки, та застосування чистих стратегій не забезпечує відшукання оптимального розв’язку гри. У такому випадку оптимальний розв’язок можна отримати у змішаних стратегіях, які одержують шляхом випадкового чередування чистих стратегій згідно із заданими ймовірностями у результаті багатократного повторення гри.

Вектор 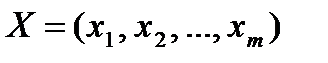з невід’ємними компонентами 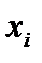, для яких виконується умова

, (5.4)

називається змішаною стратегією гравця .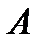

Аналогічно, змішаною стратегією гравця будемо називати вектор з невід’ємними компонентами , для яких виконується умова:

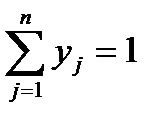. (5.5)

Якщо гравець 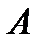буде використовувати змішану стратегію 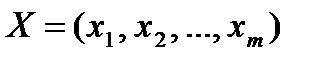, то це означає, що з ймовірністю 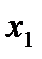він використовує першу чисту стратегію, із ймовірністю - другу чисту стратегію і т.д.

У випадку, коли гравець користується змішаною стратегією, а суперник тільки чистою -ою стратегією, то середній виграш гравця становитиме:

.

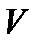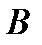Допустимо, що гравець використовує свою оптимальну змішану стратегію, а - поки що невідома ціна гри. При довільній чистій -ій стратегії гравця гравець 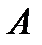забезпечить собі виграш, не менший за . З урахуванням того, що гравець 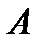намагається максимізувати свій виграш, стає очевидним, що для знаходження оптимальної змішаної стратегії 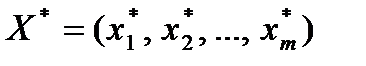необхідно знайти розв’язок такої задачі лінійного програмування:

, (5.6)

(5.7)

, (5.8)

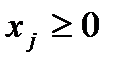, . (5.9)

Згідно основної теореми теорії матричних ігор відомо, що кожна кінцева парна гра з нульовою сумою має принаймі один розв’язок – пару оптимальних стратегій, в загальному випадку змішаних, і відповідну ціну гри.

Якщо один із гравців застосовує оптимальну змішану стратегію, то його виграш гарантовано буде не меншим за ціну гри, незалежно від стратегій, вибраних його противником.

Ціна гри є невідомою, але її можна вважати додатною. Це виходить з того, що якщо всі елементи платіжної матриці збільшити на константу, то це не вплине на зміну оптимальних стратегій (на константу збільшиться лише ціна гри).

За рахунок простих перетворень задачу (5.6) – (5.9) зводемо до стандартного вигляду задачі лінійного програмування.

Розділивши обидві частини системи нерівностей (5.7) на величину 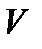отримаємо:

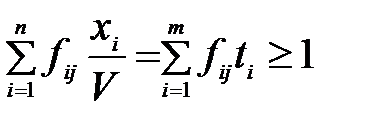, (5.10)

де прийнято таке позначення

, .

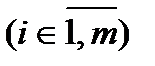Тоді, з урахуванням заміни змінної величини з умови (5.8) отримаємо:

.

З останньої рівності знаходимо:

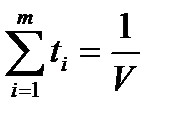. (5.11)

На підставі (5.10), (5.11) задачу (5.6) – (5.9) зведемо до вигляду:

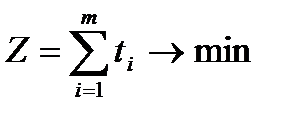(5.12)

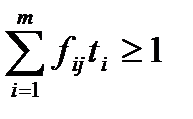, , (5.13)

, (5.14)

Для задачі (5.12) – (5.14) існує така двоїста задача лінійного програмування:

, (5.15)

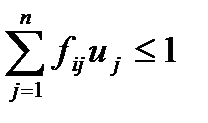, , (5.16)

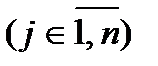, (5.17)

Нехай 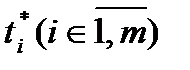та 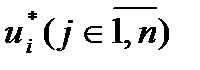- відповідно оптимальні розв’язки задач (5.12) – (5.14) та (5.15) – (5.17). Тоді компоненти векторів оптимальних змішаних стратегій гравців знаходять за такими формулами:

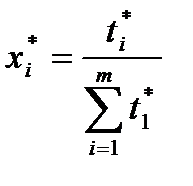; (5.18)

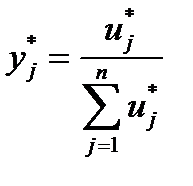. (5.19)

Значення величини 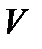можна розрахувати за такою формулою:

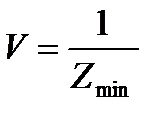, (5.20)

де 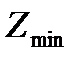- значення цільової функції задачі лінійного програмування (5.12) – (5.14) для оптимального плану.

Нагадаємо, що у випадку збільшення елементів платіжної матриці на константу, на цю ж константу необхідно відкоригувати значення ціни гри.

Розмірність платіжної матриці парної гри з нульовою сумою можна зменшити шляхом виключення стратегій, над якими існують домінуючі.

Якщо в платіжній матриці всі елементи і -го рядка є більшими або рівними відповідним елементам k -го рядка, то і -та стратегія гравця 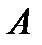є домінуючою над k -ою. У випадку, коли всі елементи 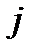-го стовпця платіжної матриці є меншими або рівними ою над 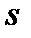-ою. Тому перед тим, як приступати до знаходження оптимальних стратегій, потрібно спробувати спростити гру шляхом аналізу платіжної матривідповідним елементам 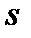-го стовпця, то 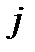-та стратегія гравця В вважається домінуючці і вилучення заздалегідь невигідних стратегій.

► Приклад 5.2. ¹ Дві фірми (в подальшому будемо ідентифікувати їх як 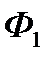і ) виробляють однорідний сезонний товар, який користується попитом протягом 5-ти тижнів. Дохід від продажу товару за тиждень становить С тис.грн. Фірма 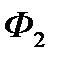, будучи більш сильною, в процесі конкурентної боротьби намагається витіснити фірму 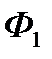з ринку збуту, прагнучи своїми діями мінімізувати доходи фірми , не рахуючись при цьому з тимчасовими втратами частини свого доходу з надією надолужити втрачене в майбутньому. Діюче законодавство забороняє застосовувати демпінгові ціни. Єдиним допустимим способом досягнення своєї цілі для фірми (як і для фірми 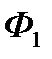в цілях захисту своїх інтересів на ринку збуту) залишаються підвищення якості товару і вдалий вибір моменту поставки його на ринок збуту. Рівень попиту на товар залежить від його якості, причому в кожний момент часу реалізується той товар, якість якого вища.

Для того, щоб покращити якість товару потрібні додаткові затрати часу на вдосконалення технології його виготовлення і переналагодження обладнання. У зв’язку з цим, вважається, що якість товару тим вища, чим пізніше він поступить на ринок.

1. Экономико–математические методы и модели. Учебн.пособие Н.И.Холод, А.В.Кузнецов и др. /Под общ.ред. А.В.Кузнецова. – Мн.: БГЭУ, 1999. – 413 с.

Необхідно визначити оптимальні стратегії кожної із фірм.

Представимо конфліктну ситуацію у вигляді парної гри з нульовою сумою.

Будемо вважати, що фірма 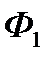поставить на ринок свій товар у момент (тиждень) і, а фірма 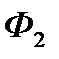- в момент 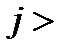і. У такому випадку фірма не буде мати конкурента на ринку протягом і) тижнів і отримає за цей період дохід у розмірі 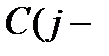і) тис.грн. У момент на ринку з’являється товар фірми , який є більш якісним (так як 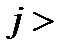і, тобто випущений пізніше), і фірма 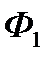втрачає ринок і доходів не отримує.

У випадку, коли і 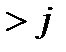, фірма 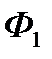, пропонуючи товар більш високої якості, буде одноособово отримувати дохід на відрізку часу від і до 5, тобто протягом (5- і +1) тижнів. Дохід фірми 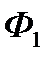на цьому відрізку буде становити С (5- і +1) тис.грн.

При і на ринок одночасно поступає товар обох фірм, який користується однаковим попитом. Тому доходи фірми і фірми будуть однаковими і складуть по 0,5С (5- і +1) тис.грн.

Формалізуємо конфліктну ситуацію у термінах теорії ігор.

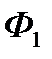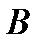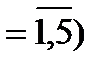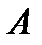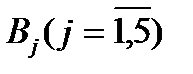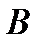Фірми і приймемо відповідно за гравців і . Позначимо через (і чисту і -ту стратегію гравця , яка полягає в тому, що він поставив свій товар на ринок збуту в і -ий тиждень, а через - чисту -ту стратегію гравця , у відповідності з якою він поставляє свій товар для реалізації в -тий тиждень.

Гравець , вибираючи час поставки товару на ринок в і -ий тиждень, намагається максимізувати свій дохід, а гравець , вибираючи 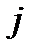-ий тиждень для поставки свого товару, має прямо протилежну ціль – мінімізувати дохід гравця . У цьому проявляється антагоністичність дій між гравцями.

Величину доходів фірми для всіх можливих випадків можна представити за допомогою такої функції виграшу:

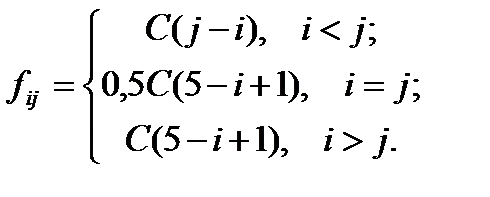
Платіжна матриця набере вигляду, поданного у табл.5.3.

Таблиця 5.3

Початкова платіжна матриця

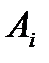
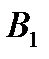
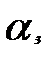
	2,5 С	С	2 С	3 С	4 С	С
	4 С	2 С	С	2 С	3 С	С
	3 С	3 С	1,5 С	С	2 С	С
	2 С	2 С	2 С	С	С	С
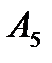
	С	С	С	С	0,5 С	0,5 С
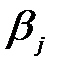
	4С	3С	2С	3С	4 С

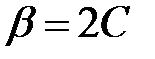
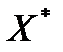Так як , то розв’язок гри у чистих стратегіях не існує. Для пошуку оптимальних змішаних стратегій і 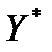спростимо платіжну матрицю. Помножимо усі елементи платіжної матриці на 1/С і в результаті отримаємо стратегічно еквівалентну матрицю (табл.5.4).

Таблиця 5.4

Перетворена платіжна матриця

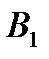
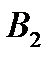
	2,5
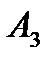
			1,5
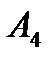
					0,5

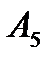У табл.5.4 елементи четвертної стрічки не менші за відповідні елементи п’ятої стрічки, тому стратегія є домінуючою над . Вилучаємо п’яту стрічку і приходимо до платіжної матриці, поданої у табл.5.5.

Таблиця 5.5

Перетворена платіжна матриця із врахуванням домінуючих стратегій

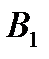
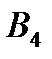
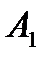
	2,5
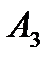
			1,5

Так як елементи другого стовпчика останньої матриці (табл.5.5) не більші за відповідні елементи першого, то перший стовпчик можна опустити.

Елементи четвертого стовпчика не більші за елементи п’ятого, тому п’ятий вилучаємо (табл.5.6).

Таблиця 5.6

Платіжна матриця для побудови задачі лінійного програмування

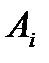
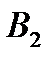
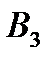
		1,5

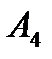
З метою знаходження оптимальної змішаної стратегії гравця 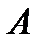складемо таку задачу лінійного програмування:

,

,

,

,

.

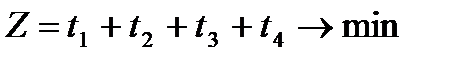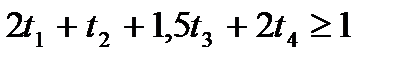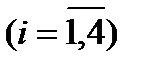Розв’язок задачі знаходимо за допомогою стандартної функції системи EXCEL Поиск решения (Сервис, Поиск решения…):

;

.

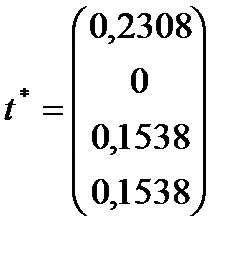Для знаходження оптимальної змішаної стратегії другого гравця потрібно розв’язати таку задачу лінійного програмування:

,

,

,

,

.

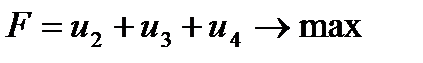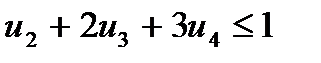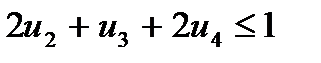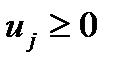
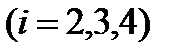В результаті розв’язання цієї задачі отримуємо:

;

.

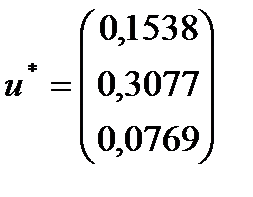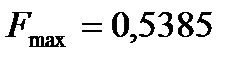Для знаходження оптимальних змішаних стратегій гравців і ціни гри скористаємося співвідношеннями (5.11), (5.18) і (5.19):

;

;

.

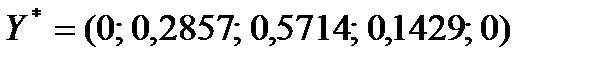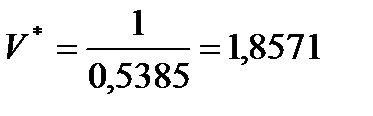Висновок: фірма повинна поставляти свій товар на ринок у перший, третій і четвертий тижні відповідно з частотами (ймовірностями) 0,4286, 0,2857 і 0,2857 і зовсім не поставляти у другий і п’ятий тиждень. Математичне сподівання доходу буде рівним 1,8571 С тис.грн.

Фірмі необхідно поставляти свій товар на ринок у другий, третій і четвертий тижні з ймовірностями відповідно 0,2857, 0,5714 і 0,1429 і не робити поставок у перший і п’ятий тиждень. ◄

Парна гра з нульовою сумою має ряд недоліків, які звужують межі її практичного застосування. До таких недоліків слід віднести:

• моделюються тільки суто антагоністичні ситуації, проте в переважній більшості виробничих ситуацій інтереси учасників просто не співпадають, а не є антагоністичними;

• гравці мають однакову інформаційну базу щодо конфліктної ситуації, хоча насправді економічні суб’єкти можуть характеризуватися різним ступенем поінформованості про суперника;

• робиться передбачення, що кожному учасникові гри відомі всі можливі стратегії його суперника, хоча у багатьох реальних випадках найкращим вирішенням ситуації може бути пошук невідомої для суперника стратегії;

• використання змішаних стратегій передбачає багатократне повторення конфліктної ситуації, в зв’язку з чим розв’язок у змішаних стратегіях не може служити рекомендацією для прийняття одноразових рішень;

• передбачається, що при багатократному повторенні конфліктних ситуацій кількість стратегій гравців і функція платежів є незмінними, що не завжди відповідає реальній дійсності.

Очевидно, що застосування апарату теорії ігор вимагає приведення конфліктної ситуації до формалізованої гри, причому без суттєвих втрат реальних цілей і умов. На жаль, у багатьох випадках представити конфліктну ситуацію у вигляді моделі матричної гри з нульовою сумою не вдається. Тому ОПР змушена використовувати інші класи ігрових моделей. Разом з тим їх побудова і методи розв’язання суттєво ускладнюються.

Дата добавления: 2014-11-29