Показники варіації та формули для їх розрахунку

Характеристики вимірювання варіації ознак - абсолютні та відносні міри варіації (розмах варіації, середнє лінійне та середнє квадратичне відхилення, коефіцієнти варіації). Варіація альтернативної ознаки

Варіація, тобто коливання, мінливість будь-якої ознаки є властивістю статистичної сукупності. Здатність ознаки змінювати індивідуальні значення називається варіабельністю. Вона зумовлена дією безлічі взаємопов’язаних причин, серед яких є основні та другорядні. Основні причини формують центр розподілу. Другорядні причини впливають на форму розподілу.

Для виміру та оцінки варіації використовують систему абсолютних та відносних характеристик. До абсолютних характеристик належать: розмах варіації, середнє лінійне відхилення, середнє квадратичне відхилення та дисперсія. До відносних характеристик варіації належать різноманітні коефіцієнти, найбільш поширене використання серед яких мають коефіцієнти варіації, що побудовані на відношенні абсолютних характеристик з середньою арифметичною. Кожна з названих характеристик має певні аналітичні переваги під час вирішення тих чи інших завдань статистичного аналізу.

Методика обчислення характеристик варіації залежить від виду ознаки Х та наявних даних (первинні чи похідні, згруповані чи ні).

Розмах варіації – різниця між найбільшим і найменшим значеннями ознаки, розраховується за формулою:

R = X _max – X _min,

де X _max – максимальне значення ознаки;

X _min – мінімальне значення ознаки.

Розмах варіації характеризує межі, в яких змінюється кількісне значення ознаки. Цей показник встановлює крайні числові значення варіант, що складають досліджувану сукупність.

В інтервальному ряді розподілу розмах варіації визначають як різницю між верхньою межею останнього інтервалу та нижньою межею першого. Проте, якщо інтервал відкритий, для обчислення розмаху варіації використовується середина інтервалу. Звичайно, спочатку інтервал має бути закритим згідно з відповідними правилами.

Крім розмаху варіації, у практиці статистичного аналізу широко застосовують інші абсолютні характеристики варіації, що ґрунтуються на відхиленнях індивідуальних значень ознаки від середньої арифметичної.

Оскільки відповідно до першої властивості середньої арифметичної å (Х _і – ) = 0, то при розрахунку такого роду характеристик використовують або модулі, або квадрати відхилень. У результаті маємо такі характеристики варіації: середнє лінійне відхилення, середнє квадратичне відхилення та дисперсію. Розрахункові формули цих показників наведені в табл. 6.5.

Якщо статистична сукупність надана у вигляді інтервального варіаційного ряду, то для розрахунку показників варіації використовуються розрахункові формули за зваженою формою. При цьому замість індивідуального значення ознаки обирається середина відповідного інтервалу.

Середнє лінійне відхилення являє собою середню відстань між середньою арифметичною величиною та відповідними індивідуальними значеннями окремих ознак, а це завжди додатна величина. Саме тому у формулах відхилення кожної варіанти від середньої арифметичної береться за модулем.

Таблиця 6.5

Назва показника	Розрахункова формула за даними
не згрупованими	згрупованими
Середнє лінійне відхилення
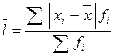
Середнє квадратичне відхилення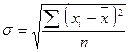
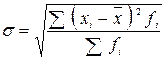
Дисперсія
хі – індивідуальні значення окремої ознаки, варіанти; 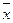– середня арифметична (середнє значення ознаки); n – обсяг сукупності, кількість ознак у сукупності; fi – частота відповідної ознаки.

Дисперсія являє собою середній квадрат відхилень, є відповідні властивості дисперсії і вона пов’язана з середнім квадратичним відхиленням таким співвідношенням:

,

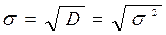де s – середнє квадратичне відхилення;

D = s ² – дисперсія.

При порівнянні варіації різних ознак або однієї ознаки у різних сукупностях використовуються відносні характеристики: коефіцієнти варіації. До них належать:

· лінійний коефіцієнт варіації, який обчислюється за формулою:

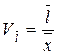, або ·100 %,

де 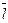– середнє лінійне відхилення;

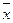– середня арифметична;

· квадратичний коефіцієнт варіації, який обчислюється за формулою:

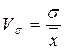, або 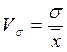·100 %,

де s – середнє квадратичне відхилення;

· коефіцієнт осциляції, який обчислюється за формулою:

,

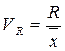де R – розмах варіації.

Чим менше середнє відхилення, тим більш типова середня, тим більш однорідна сукупність. Найчастіше квадратичний коефіцієнт варіації використовують як критерій однорідності сукупності, він є ознакою надійності середньої.. У симетричному, близькому до нормального, розподілі V_σ = 0,33.

Для малих сукупностей розрізняють такі значення відносних коливань:

V_σ < 10% - незначне коливання, сукупність однорідна, значення середньої є типовим рівнем ознаки в даній сукупності;

10 % ≤ V_σ ≤ 33% - середнє коливання, сукупність в межах однорідності, значення середньої можна вважати типовим рівнем ознаки в даній сукупності;

V_σ > 33% - високий рівень варіації, сукупність неоднорідна, значення середньої неможна вважати типовим рівнем ознаки в даній сукупності.

Дисперсія альтернативної ознаки обчислюється як добуток часток за формулою:

,

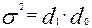де d ₁ – частка елементів сукупності, яким властива ознака;

d ₀ – частка решти елементів, у яких відсутня ознака (d ₀ = 1 – d ₁).

Дисперсія альтернативної ознаки широко використовується під час проектування вибіркових обстежень, обробці даних соціологічних опитувань, статистичному контролі якості продукції тощо.

Дата добавления: 2014-12-07