Характеристики форми розподілу: коефіцієнти асиметрії та ексцесу

Різноманітність статистичних сукупностей – передумова різних форм співвідношення частот і значень варіативної ознаки. За своєю формою роз-поділи поділяються на одновершинні (див. рис. 6.7) та багатовершинні (коли розподіл має дві, три та більше вершин). Наявність двох і більше вершин (див. рис. 6.8) свідчить про неоднорідність сукупності, про поєднання в ній груп з різними рівнями ознаки. У такому разі необхідно більш ретельно проаналізувати наявну вихідну інформацію, перегрупувати дані, виділивши однорідні групи. Розподіли якісно однорідних сукупностей, як правило, одновершинні. Серед одновершинних розподілів є симетричні та асиметричні (скошені), гостровершинні та плосковершинні.

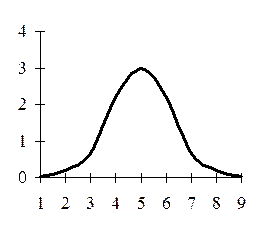
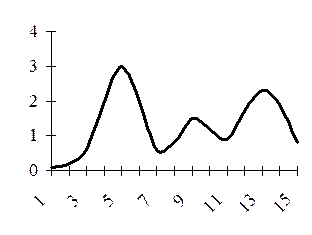
Рис.6.7. Одновершинний розподіл Рис. 6.8. Багатовершинний розподіл

У симетричному розподілі рівновіддалені від центра значення ознаки мають однакові частоти, при цьому середня, мода та медіана мають однакові значення = Мо = Ме; в асиметричному – вершина розподілу зміщена. Напрям асиметрії протилежний напряму зміщення вершини. Якщо вершина зміщена вліво, то це правостороння асиметрія. У цьому випадку > Me > Mo. Якщо вершина зміщена вправо, то це лівостороння асиметрія. В цьому випадку 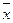< Me < Mo. Асиметрія (див. рис. 6.9) виникає внаслідок обмеженої варіації в одному напрямі або під впливом домінуючої причини розвитку, яка веде до зміщення центру розподілу. Очевидно, що в симетричному розподілі А = 0, при правосторонній асиметрії A > 0, при лівосторонній – A < 0.

Найпростішою мірою асиметрії є відхилення від середньої арифметичної медіани чи моди. В симетричному розподілі характеристики центра мають однакові значення 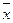= Мо = Ме; в асиметричному – між ними існують певні розбіжності.

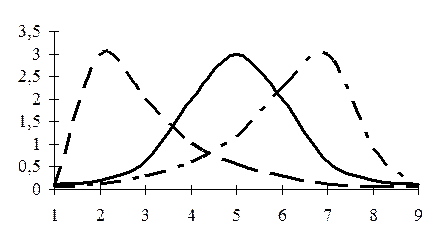
Рис. 6.9. Види розподілу:

- симетричний розподіл (Мо = Ме = );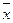

- правостороння (додатня) асиметрія (Мо < Ме < );

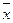– - лівостороння (від’ємна) асиметрія (Мо > Ме > ).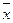

Стандартизовані відхилення, які мають назву коефіцієнта асиметрії, характеризують напрям та міру скошеності розподілу і розраховуються за формулами:

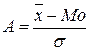або. ;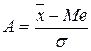

Якщо має місце відхилення коефіцієнта асиметрії від нуля в той чи інший бік, то можна вести мову про більшу чи меншу асиметрію. Вважають, що при 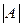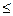0,25 асиметрія низька; при 0,25<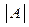 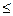0,5 - помірна, або середня; при 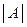> 0,5 - асиметрія висока.

Характеристики центру розподілу ґрунтуються на моментах розподілу. Момент розподілу – це середня k -го ступеня відхилень 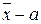. Залежно від величини а моменти поділяють на первинні (а = 0), центральні 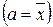і умовні (a = const). Ступінь k визначає порядок моменту. В загальному вигляді центральний момент k -го порядку розраховується за формулою:

,

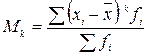де х_і – значення окремої варіанти;

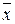– середня арифметична;

k – ступінь моменту;

f_i – частота окремої варіанти.

Для того, щоб характеристика скошеності не залежала від масштабу вимірювання ознаки для порівняння ступеня асиметрії різних розподілів, використовують стандартизований момент третього ступеня. В такому разі коефіцієнт асиметрії визначається за формулою:

,

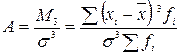де М₃ – центральний момент третього порядку;

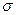– середнє квадратичне відхилення.

Гостровершинність розподілу відображає скупченість значень ознаки навколо середньої величини та називається ексцесом. Для вимірювання ексцесу використовують коефіцієнт, побудований за допомогою стандартизованого моменту четвертого порядку, який розраховується за формулою:

,

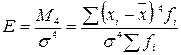де М₄ – центральний момент четвертого порядку.

Якщо Е = 3, то розподіл уважається нормальним, при E < 3 – плосковершинний, при E > 3 - розподіл має гостровершинну форму. Термін «ексцес» грецького походження (kurtosis), тому назви форми ексцесу походять від цього кореня слова (див. рис.6.10):

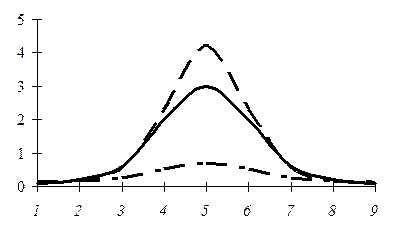
Рис.6.10. Види розподілу:

– нормальний (мезокуртичний) (Е = 3);

– гостровершинний (стрічкокуртичний) (Е > 3);

– плосковершинний (платокуртичний) (Е < 3).

Наведений графік свідчить, що для стрічкокуртичної кривої характерне розміщення більшості одиниць сукупності поблизу центра. У випадку платокуртичної кривої (форма силуету – плато) варіанти значно віддалені від центру розподілу. Помірне розміщення навколо центра розподілу варіант визначає форма ексцесу у вигляді мезокуртичної кривої. На практиці часто в одному розподілі поєднуються всі названі особливості, а саме: одновершинний розподіл може бути симетричним та гостровершинним, або плосковершинним з лівосторонньою асиметрією, або гостровершинним з правосторонньою асиметрією тощо.

Дата добавления: 2014-12-07