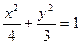КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Образец решения контрольной работы № 1
|
|
|
|
Задание 1. Даны вершины А (–1; 0), В (5; 2), С (2; 4) треугольника ABC. Найти: 1) длину стороны АВ; 2) уравнение медианы CM, проведенной из вершины С; 3) уравнение высоты СH, проведенной из вершины С; 4) уравнение прямой L, проходящей через вершину С параллельно стороне АВ; 5) длину высоты СH; 6) величину внутреннего угла А. Сделать чертеж.
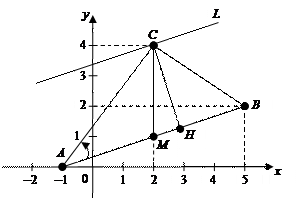 Решение. Изобразим заданный треугольник в декартовой системе координат Oxy.
Решение. Изобразим заданный треугольник в декартовой системе координат Oxy.
 |
1) Длину стороны АВ найдем, используя формулу расстояния между двумя точками на плоскости: 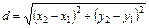 .
.
Подставляя в нее координаты точек А (–1; 0) и В (5; 2), получим: 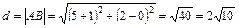 (ед.).
(ед.).
2) По определению медианы точка М медианы CМ делит сторону АВ пополам. Следовательно, ее координаты определяются по формулам деления отрезка пополам:
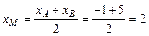 ,
, 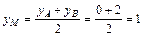 .
.
Таким образом, найдена точка М (2; 1).
Уравнение медианы CМ найдем как уравнение прямой, проходящей через две заданные точки C и М, по формуле: 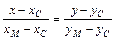 или
или 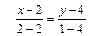 , или
, или 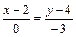 .
.
По свойству пропорции отсюда следует уравнение CМ:
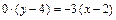 или
или 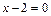 .
.
3) Уравнение высоты СH как прямой, проходящей через точку С перпендикулярно стороне АВ, будем искать в виде 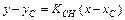 , где угловой коэффициент
, где угловой коэффициент 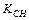 найдем из условия перпендикулярности прямых СH и АВ:
найдем из условия перпендикулярности прямых СH и АВ: 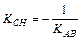 .
.
Угловой коэффициент 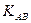 определим, используя формулу углового коэффициента прямой:
определим, используя формулу углового коэффициента прямой: 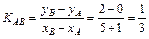 . Следовательно,
. Следовательно, 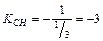 .
.
Уравнение высоты примет теперь вид: 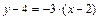 или
или 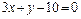 .
.
4) Аналогично, уравнение прямой L, проходящей через вершину С параллельно стороне АВ, будем искать в виде: 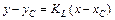 , где угловой коэффициент
, где угловой коэффициент 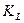 прямой L найдем из условия параллельности прямых L и AB:
прямой L найдем из условия параллельности прямых L и AB: 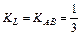 .
.
Уравнение прямой L примет вид: 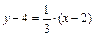 или
или 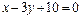 .
.
5) Длину высоты СН найдем, используя формулу расстояния от точки С до прямой АВ: 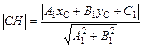 , где
, где 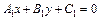 есть общее уравнение стороны АВ.
есть общее уравнение стороны АВ.
Найдем уравнение стороны АВ: 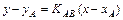 или
или 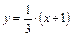 , или
, или 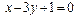 .
.
Подставляя в найденное уравнение координаты точки С, получим: 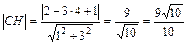 (ед.).
(ед.).
6) Из рисунка видно, что внутренний угол А треугольника АВС есть угол, на который нужно повернуть сторону АВ в положительном направлении (т. е. против часовой стрелки) до совмещения ее со стороной АС. Поэтому тангенс угла А найдем по формуле: 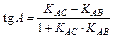 .
.
Угловой коэффициент 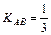 (найден в п. 3). Аналогично найдем
(найден в п. 3). Аналогично найдем 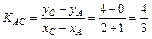 . Следовательно,
. Следовательно, 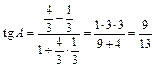 , тогда
, тогда 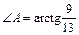 (рад.).
(рад.).
Ответ: 1) длина стороны АВ: 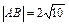 ед.; 2) уравнение медианы CМ:
ед.; 2) уравнение медианы CМ: 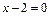 ; 3) уравнение высоты СН:
; 3) уравнение высоты СН: 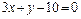 ; 4) уравнение прямой L:
; 4) уравнение прямой L: 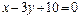 ; 5) длина высоты СН:
; 5) длина высоты СН: 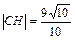 ед.; 6) величина внутреннего угла А:
ед.; 6) величина внутреннего угла А: 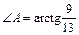 рад.
рад.
Задание 2. Составить уравнение и построить линию, для каждой точки которой выполняется следующее условие: отношение расстояний до точки F (–1; 0) и прямой 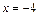 равно
равно 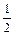 .
.
Решение. Сделаем схематический чертеж по условию задачи.
 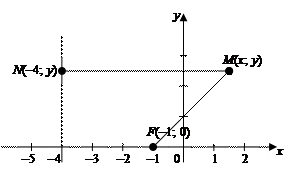 |
1) Предположим, что М (x; y) – текущая точка искомой линии. Тогда точка N (–4; y) является ее проекцией на прямой x = –4.
2) По условию задачи выполняется следующее отношение расстояний: 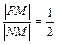 или
или 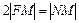 .
.
3) Используя формулу расстояния между двумя точками, выразим полученное буквенное равенство в координатной форме и преобразуем его к виду канонического уравнения одной из кривых второго порядка (окружности, эллипса, гиперболы или параболы):
|
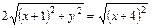 или
или 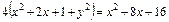 , или
, или 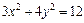 .
.
Получили каноническое уравнение эллипса: 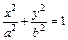 , у которого полуоси есть
, у которого полуоси есть 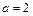 и
и 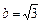 .
.
4) Построим линию по ее уравнению.
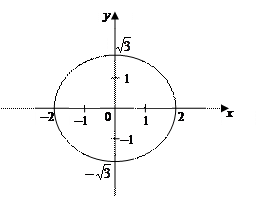
Ответ: 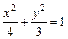
 эллипс.
эллипс.
Задание 3. Написать разложение вектора 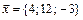 по векторам
по векторам 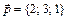 ,
, 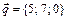 ,
, 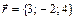 .
.
Решение. Требуется представить вектор 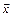 в виде
в виде 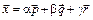 , где a, b и g – неизвестные числа. Согласно определения произведения вектора на число и суммы векторов имеем:
, где a, b и g – неизвестные числа. Согласно определения произведения вектора на число и суммы векторов имеем: 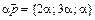 ,
, 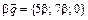 ,
, 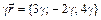 и
и 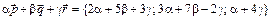 . Применяя определение равенства двух векторов получим линейную систему трех уравнений относительно неизвестных a, b, g:
. Применяя определение равенства двух векторов получим линейную систему трех уравнений относительно неизвестных a, b, g: 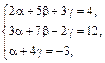 которую решим по формулам Крамера. Для этого составим четыре определителя 3-го порядка и вычислим их по правилу треугольников:
которую решим по формулам Крамера. Для этого составим четыре определителя 3-го порядка и вычислим их по правилу треугольников:
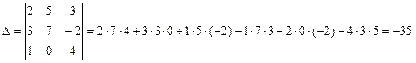 .
.
Т. к. 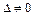 , то система имеет единственное решение.
, то система имеет единственное решение.
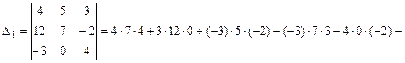
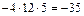 .
.
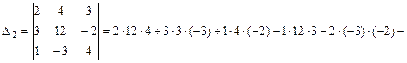
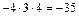 .
.
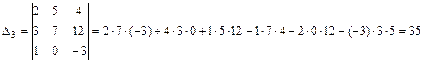 .
.
Т. о., по формулам Крамера: 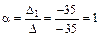 ,
,  ,
, 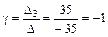 .
.
Ответ: 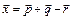 .
.
Задание 4. Даны вершины A 1(1; –1; 2), A 2(2; 1; 2), A 3(1; 1; 4),
A 4(6; –3; 8) пирамиды A 1 A 2 A 3 A 4. Найти: 1) величину угла между ребрами A 1 A 3 и A 1 A 4; 2) площадь грани A 1 A 2 A 3; 3) уравнение плоскости, содержащей грань A 1 A 2 A 3; 4) уравнение высоты пирамиды, проведенной через вершину A 4. Сделать схематический чертеж.
 Решение. Сделаем схематический чертеж.
Решение. Сделаем схематический чертеж.
1) Найдем векторы 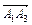 и
и 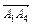 , проходящие через 2 заданные точки:
, проходящие через 2 заданные точки:
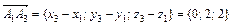 ,
,
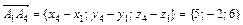 .
.
Находим косинус угла между векторами по формуле:
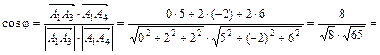
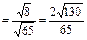 . Следовательно,
. Следовательно, 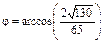 (рад.).
(рад.).
2) Гранью A 1 A 2 A 3 пирамиды A 1 A 2 A 3 A 4 является треугольник A 1 A 2 A 3, площадь которого определим по формуле: 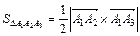 .
.
Координаты вектора 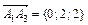 (см. п. 1). Аналогично найдем координаты вектора
(см. п. 1). Аналогично найдем координаты вектора 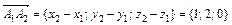 .
.
Вычислим теперь векторное произведение векторов 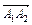 и
и 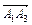 :
:
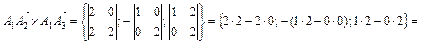
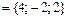 .
.
Тогда длина векторного произведения равна:
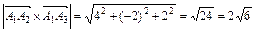 .
.
Т. о., получим: 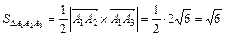 (кв. ед.).
(кв. ед.).
3) Уравнение искомой плоскости составим как уравнение плоскости, проходящей через три данные точки A 1, A 2, A 3 в форме определителя 3-го порядка: 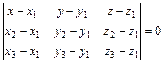 или
или 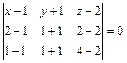 , или
, или 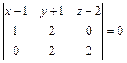 , или
, или 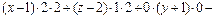
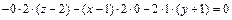 , или
, или 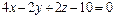 , или
, или 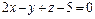 .
.
4) Уравнение высоты, опущенной из точки А 4 на грань А 1 А 2 А 3 найдем как прямую, проходящую через точку А 4 перпендикулярно плоскости А 1 А 2 А 3 в форме канонических уравнений прямой 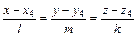 , где вектор
, где вектор 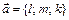 является направляющем вектором прямой (коллинеарен прямой). В п. 3 было найдено уравнение плоскости А 1 А 2 А 3:
является направляющем вектором прямой (коллинеарен прямой). В п. 3 было найдено уравнение плоскости А 1 А 2 А 3: 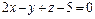 , следовательно, ее нормальным вектором является вектор
, следовательно, ее нормальным вектором является вектор 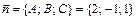 . Т. к. вектор
. Т. к. вектор 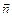 коллинеарен высоте, то его можно выбрать в качестве направляющего вектора
коллинеарен высоте, то его можно выбрать в качестве направляющего вектора 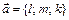 прямой. Следовательно, искомое уравнение высоты имеет вид:
прямой. Следовательно, искомое уравнение высоты имеет вид: 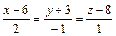 .
.
Ответ: 1) величина угла между ребрами A 1 A 3 и A 1 A 4: 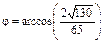 рад.; 2) площадь грани A 1 A 2 A 3:
рад.; 2) площадь грани A 1 A 2 A 3: 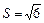 кв. ед.; 3) уравнение плоскости A 1 A 2 A 3:
кв. ед.; 3) уравнение плоскости A 1 A 2 A 3: 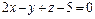 ; 4) уравнение высоты из вершины A 4:
; 4) уравнение высоты из вершины A 4: 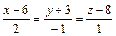 .
.
2.1. Контрольная работа № 2. «Введение в анализ. Дифференциальное исчисление».
1. Найти пределы функций.
1. 1) 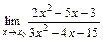 при: а)
при: а) 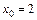 ; б)
; б) 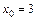 ; в)
; в) 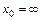 ;
;
2) 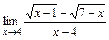 ; 3)
; 3) 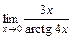 .
.
2. 1) 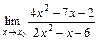 при: а)
при: а) 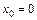 ; б)
; б) 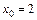 ; в)
; в) 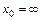 ;
;
2) 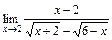 ; 3)
; 3) 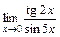 .
.
3. 1) 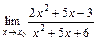 при: а)
при: а) 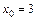 ; б)
; б) 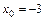 ; в)
; в) 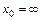 ;
;
2) 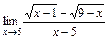 ; 3)
; 3) 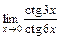 .
.
4. 1) 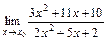 при: а)
при: а) 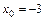 ; б)
; б) 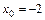 ; в)
; в) 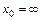 ;
;
2) 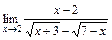 ; 3)
; 3) 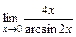 .
.
5. 1) 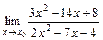 при: а)
при: а) 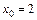 ; б)
; б) 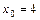 ; в)
; в) 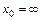 ;
;
2) 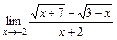 ; 3)
; 3) 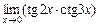 .
.
6. 1) 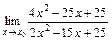 при: а)
при: а) 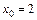 ; б)
; б) 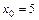 ; в)
; в) 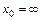 ;
;
2) 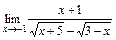 ; 3)
; 3) 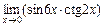 .
.
7. 1) 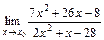 при: а)
при: а) 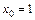 ; б)
; б) 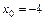 ; в)
; в) 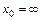 ;
;
2) 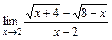 ; 3)
; 3) 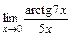 .
.
8. 1) 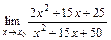 при: а)
при: а) 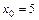 ; б)
; б) 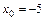 ; в)
; в) 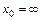 ;
;
2) 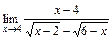 ; 3)
; 3) 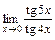 .
.
9. 1) 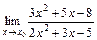 при: а)
при: а) 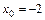 ; б)
; б) 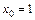 ; в)
; в) 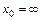 ;
;
2) 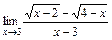 ; 3)
; 3) 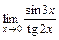 .
.
10. 1) 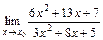 при: а)
при: а) 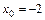 ; б)
; б) 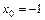 ; в)
; в) 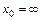 ;
;
2) 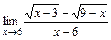 ; 3)
; 3) 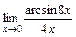 .
.
2. Найти производные заданных функций.
1. 1) 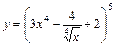 ; 2)
; 2) 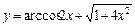 ;
;
3) 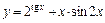 .
.
2. 1) 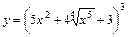 ; 2)
; 2) 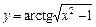 ;
;
3) 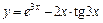 .
.
3. 1) 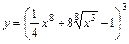 ; 2)
; 2) 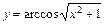 ;
;
3) 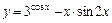 .
.
4. 1) 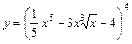 ; 2)
; 2) 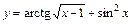 ;
;
3) 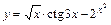 .
.
5. 1) 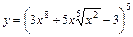 ; 2)
; 2) 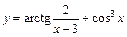 ;
;
3) 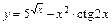 .
.
6. 1) 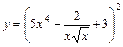 ; 2)
; 2) 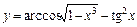 ;
;
3) 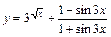 .
.
7. 1) 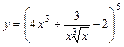 ; 2)
; 2) 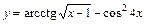 ;
;
3) 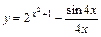 .
.
8. 1) 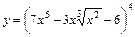 ; 2)
; 2) 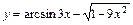 ;
;
3) 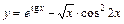 .
.
9. 1) 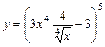 ; 2)
; 2) 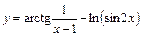 ;
;
3) 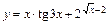 .
.
10. 1) 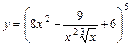 ; 2)
; 2) 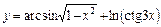 ;
;
3) 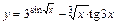 .
.
3. Провести полное исследование функции и построить ее график.
1. 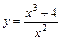 . 2.
. 2. 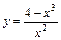 .
.
3. 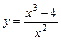 . 4.
. 4. 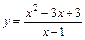 .
.
5. 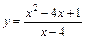 . 6.
. 6. 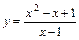 .
.
7. 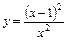 . 8.
. 8. 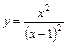 .
.
9. 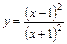 . 10.
. 10. 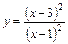 .
.
4. Доказать, что функция z = f (x; y) удовлетворяет данному уравнению.
1. 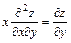 , если
, если 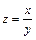 .
.
2. 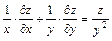 , если
, если 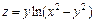 .
.
3. 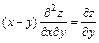 , если
, если 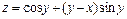 .
.
4. 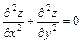 , если
, если 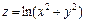 .
.
5. 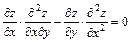 , если
, если 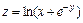 .
.
6. 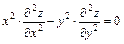 , если
, если 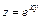 .
.
7.  , если
, если 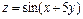 .
.
8. 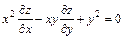 , если
, если 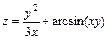 .
.
9. 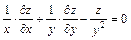 , если
, если  .
.
10. 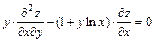 , если
, если 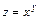 .
.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 375; Нарушение авторских прав?; Мы поможем в написании вашей работы!