
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Применение производной
|
|
|
|
Механический смысл производной
Геометрический смысл производной
22. Производная от функции 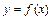 в точке
в точке 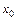 равна угловому коэффициенту (т. е. тангенсу угла наклона) касательной, проведенной к графику функции
равна угловому коэффициенту (т. е. тангенсу угла наклона) касательной, проведенной к графику функции 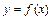 в точке
в точке 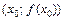 (рис. 7). Уравнение касательной:
(рис. 7). Уравнение касательной:  . Уравнение нормали:
. Уравнение нормали: 

Рис. 7
23. Производная от функции 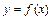 в точке
в точке 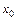 численно равна скорости изменения функции
численно равна скорости изменения функции 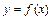 в момент
в момент  .
.
24. Если функция задана параметрически уравнениями  то производная вычисляется по формуле:
то производная вычисляется по формуле:  . Вторая производная находится по формуле:
. Вторая производная находится по формуле:  .
.
25. Если функция задана неявно уравнением 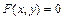 , то для нахождения ее производной дифференцируют обе части этого уравнения, считая
, то для нахождения ее производной дифференцируют обе части этого уравнения, считая 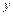 сложной функцией от
сложной функцией от 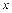 и полученное уравнение разрешают относительно
и полученное уравнение разрешают относительно  .
.
26. Если на некотором промежутке 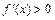 , то на этом промежутке функция
, то на этом промежутке функция  возрастает; если
возрастает; если  , то функция убывает.
, то функция убывает.
27. Если функция  непрерывна в точке
непрерывна в точке  и в левой ее окрестности
и в левой ее окрестности 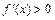 , а в правой
, а в правой  , то в точке
, то в точке  функция имеет максимум; если в левой окрестности
функция имеет максимум; если в левой окрестности  , а в правой
, а в правой 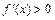 , то в точке
, то в точке  функция имеет минимум.
функция имеет минимум.
28. Если на некотором промежутке  , то на этом промежутке функция
, то на этом промежутке функция 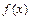 вогнута; если
вогнута; если  , то функция выпукла.
, то функция выпукла.
29. Если функция  непрерывна в точке
непрерывна в точке  и при переходе через точку вторая производная меняет знак, то точка
и при переходе через точку вторая производная меняет знак, то точка  – точка перегиба.
– точка перегиба.
30. Для нахождения наибольшего или наименьшего значения функции 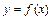 на отрезке
на отрезке 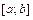 нужно:
нужно:
а) найти критические точки – точки, в которых производная функции 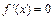 , не существует или равна бесконечности;
, не существует или равна бесконечности;
б) найти значения функции в критических точках, принадлежащие отрезку 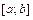 и на концах отрезка;
и на концах отрезка;
в) выбрать среди полученных чисел наибольшее или наименьшее.
31. Для исследования функции  и построения ее графика пользуются следующей схемой:
и построения ее графика пользуются следующей схемой:
а) определяется область определения функции, находятся точки разрыва, определяется их характер, находятся вертикальные асимптоты, если они есть;
б) проверяется четность, нечетность, периодичность графика, поведение его при 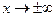 (или на границах области определения, если она ограничена); определяется наличие невертикальных асимптот вида
(или на границах области определения, если она ограничена); определяется наличие невертикальных асимптот вида 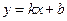 , для чего числа k и b находятся по формулам:
, для чего числа k и b находятся по формулам: 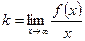 ,
, 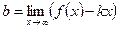 , если оба эти предела существуют и конечны;
, если оба эти предела существуют и конечны;
в) находится производная  , определяются интервалы возрастания
, определяются интервалы возрастания  , убывания
, убывания  и критические точки (
и критические точки (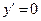 или не существует) функции, находятся экстремумы;
или не существует) функции, находятся экстремумы;
г) находится вторая производная 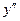 , определяются интервалы выпуклости вверх
, определяются интервалы выпуклости вверх 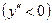 , выпуклости вниз
, выпуклости вниз 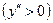 и точки перегиба графика;
и точки перегиба графика;
д) если необходимо, находятся дополнительные точки.
Сведя всю полученную информацию в таблицу, строят график функции  .
.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 719; Нарушение авторских прав?; Мы поможем в написании вашей работы!