Основные понятия. Знакопеременные и знакочередующиеся ряды

Функциональные ряды

Знакопеременные и знакочередующиеся ряды

10. Признак Лейбница. Пусть дан знакочередующийся ряд , где a_n > 0. Если 1) члены знакочередующегося ряда убывают по абсолютной величине и 2) предел его общего члена при 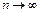равен нулю, т. е. 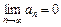, то исходный ряд сходится, а его сумма не превосходит первого члена .

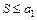11. Пусть дан знакопеременный ряд 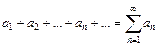. Если соответствующий ряд сходится, то данный ряд сходится абсолютно.

12. Если знакопеременный ряд 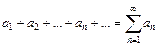сходится по признаку Лейбница, а соответствующий ряд расходится, то данный ряд сходится условно.

13. Ряд , членами которого являются функции, называется функциональным.

14. Областью абсолютной сходимости данного функционального ряда называется множество значений х, при которых данный ряд сходиться как числовой ряд.

15. Область абсолютной сходимости функционального ряда находится из неравенства .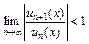

16. Степенным рядом называется ряд вида .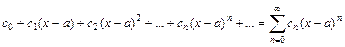

17. Радиус абсолютной сходимости степенного ряда: 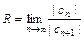или .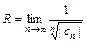

18. Интервалом абсолютной сходимости степенного ряда называется интервал вида (a – R; a + R).

19. Интервал абсолютной сходимости с исследованными границами называется областью абсолютной сходимости степенного ряда.

20. Теорема Абеля: 1) если степенной ряд сходится при значении 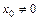, то он сходится и притом абсолютно при всех значениях х таких, что | x | < | x ₀|; 2) если степенной ряд расходится при х ₁, то он расходится при всех значениях х таких, что | x | > | x ₁|.

21. Основные свойства степенных рядов в интервале (a – R; a + R) абсолютной сходимости:

1) В интервале (a – R; a + R) сумма ряда есть непрерывная функция.

2) Степенной ряд в каждой точке интервала (a – R; a + R) можно почленно дифференцировать бесконечное число раз.

3) Степенной ряд можно почленно интегрировать по любому интервалу .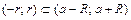

22. Ряд Тейлора для функции

23. Частный случай ряда Тейлора для функции при а = 0 – ряд Маклорена:

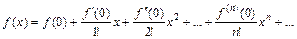
24. Разложение основных функций в ряд Маклорена:

Разложение	Область абс. сход.

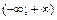
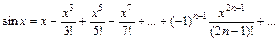
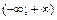
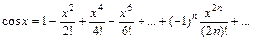
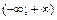
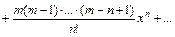
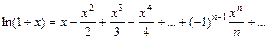
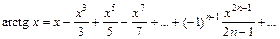
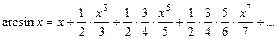
25. Тригонометрическим называется функциональный ряд вида .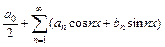

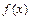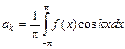26. Ряд Фурье для функции периода 2p: , где , и .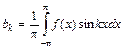

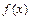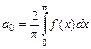27. Если – четная функция периода 2p, то ряд Фурье имеет вид , где , и .

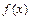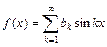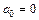28. Если – нечетная функция периода 2p, то ряд Фурье имеет вид , где , и .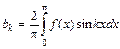

29. Условия Дирихле. Функция 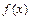на 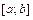ограничена и 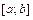можно разбить на некоторое число отрезков, на каждом из которых 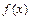была бы непрерывна и изменялась монотонно.

30. Ряд Фурье для функции 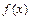, заданной на промежутке 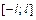: 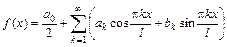, где , и .

31. Если 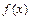– четная функция, заданная на промежутке 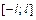, то ряд Фурье имеет вид , где , и .

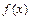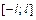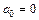32. Если – нечетная функция, заданная на промежутке , то ряд Фурье имеет вид , где , и .

Дата добавления: 2014-11-29