
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дифференциальные уравнения
Основные теоретические сведения.
1. Равенство вида 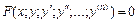 , содержащее независимую переменную x, искомую функцию y = y (x) и ее производные какого-либо порядка, называется дифференциальным уравнением.
, содержащее независимую переменную x, искомую функцию y = y (x) и ее производные какого-либо порядка, называется дифференциальным уравнением.
2. Натуральное число n, являющееся порядком старшей производной, называется порядком дифференциального уравнения.
3. Дифференциальным уравнением 1-го порядка называется уравнение вида 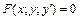 или в дифференциалах
или в дифференциалах 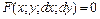 . Если эти равенства можно разрешить относительно производной, то их записывают в виде
. Если эти равенства можно разрешить относительно производной, то их записывают в виде 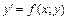 или
или 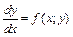 .
.
4. Решением дифференциального уравнения 1-го порядка называется функция y = j(x), имеющая непрерывную производную 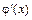 на некотором интервале (a; b) и обращающая уравнение в верное числовое равенство.
на некотором интервале (a; b) и обращающая уравнение в верное числовое равенство.
5. Задача Коши для дифференциального уравнения 1-го порядка: требуется найти решение y = j(x) уравнения, удовлетворяющее начальному условию y = y 0 при x = x 0.
6. Общим решением дифференциального уравнения 1-го порядка называется функция y = j(x; С), содержащая произвольную постоянную С и удовлетворяющая условиям: 1) при любых начальных условиях (x 0; y 0) уравнение y 0 = j(x 0; С) должно быть разрешимо относительно С так, что С = y(x 0; y 0); 2) при всех значениях постоянной С = y(x 0; y 0) функция y = j(x; y(x 0; y 0)) должна удовлетворять дифференциальному уравнению.
7. Всякое решение, получаемое из общего при фиксированном значении постоянной С называется частным решением дифференциального уравнения.
8. Уравнение вида 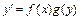 или
или 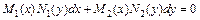 называется дифференциальным уравнением с разделяющимися переменными. Приводятся к виду
называется дифференциальным уравнением с разделяющимися переменными. Приводятся к виду 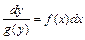 или
или 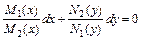 путем разделения переменных x и y и затем почленно интегрируются.
путем разделения переменных x и y и затем почленно интегрируются.
9. Уравнение вида 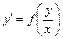 называется однородным дифференциальным уравнением. Используется замена:
называется однородным дифференциальным уравнением. Используется замена: 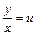 или
или 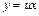 , где
, где 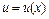 – новая неизвестная функция, тогда
– новая неизвестная функция, тогда 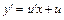 . Сводится к дифференциальному уравнению с разделяющимися переменными относительно новой функции, для которого находят общее решение. Записывают общее решение исходного уравнения по формуле
. Сводится к дифференциальному уравнению с разделяющимися переменными относительно новой функции, для которого находят общее решение. Записывают общее решение исходного уравнения по формуле 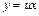 .
.
10. Уравнение вида 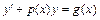 называется линейным дифференциальным уравнением. Используется метод Бернулли:
называется линейным дифференциальным уравнением. Используется метод Бернулли: 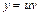 , где
, где 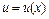 ,
, 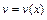 – новые неизвестные функции, тогда
– новые неизвестные функции, тогда 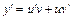 . Получаем:
. Получаем:  или
или 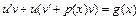 . Подберем функцию v так, чтобы выражение в скобках было равно нулю, тогда получаем
. Подберем функцию v так, чтобы выражение в скобках было равно нулю, тогда получаем 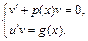 Первое уравнение – ДУ с разделяющимися переменными, находим его частное решение при С = 0. Найденное частное решение подставляем во второе уравнение, являющееся тоже ДУ с разделяющимися переменными и находим его общее решение. Записываем общее решение исходного уравнения по формуле
Первое уравнение – ДУ с разделяющимися переменными, находим его частное решение при С = 0. Найденное частное решение подставляем во второе уравнение, являющееся тоже ДУ с разделяющимися переменными и находим его общее решение. Записываем общее решение исходного уравнения по формуле 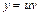 .
.
11. Уравнение вида  , где
, где 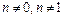 называется дифференциальным уравнением Бернулли. Используется метод Бернулли:
называется дифференциальным уравнением Бернулли. Используется метод Бернулли: 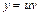 .
.
12. Дифференциальным уравнением 2-го порядка называется уравнение вида 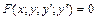 . Если уравнение можно разрешить относительно
. Если уравнение можно разрешить относительно 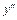 , то его записывают в виде
, то его записывают в виде 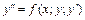 .
.
13. Решением дифференциального уравнения 2-го порядка называется функция y = j(x), имеющая непрерывные производные 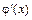 ,
, 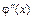 на некотором интервале (a; b) и обращающая уравнение в верное числовое равенство.
на некотором интервале (a; b) и обращающая уравнение в верное числовое равенство.
14. Задача Коши для дифференциального уравнения 2-го порядка: требуется найти решение y = j(x) уравнения, удовлетворяющее начальным условиям y = y 0,  при x = x 0.
при x = x 0.
15. Общим решением дифференциального уравнения 2-го порядка называется функция y = j(x; С 1; С 2), содержащая две произвольные постоянные С 1, С 2 и удовлетворяющая условиям: 1) при любых начальных условиях 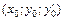 система уравнений
система уравнений 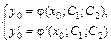 должна быть разрешима относительно постоянных С 1, С 2 так, что
должна быть разрешима относительно постоянных С 1, С 2 так, что 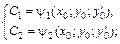 2) при всех значениях этих постоянных С 1, С 2 функция y = j(x; C 1; C 2) обращает дифференциальное уравнение в верное числовое равенство.
2) при всех значениях этих постоянных С 1, С 2 функция y = j(x; C 1; C 2) обращает дифференциальное уравнение в верное числовое равенство.
16. Всякое решение, получаемое из общего при фиксированных значениях постоянных С 1, С 2 называется частным решением дифференциального уравнения.
17. Дифференциальные уравнения 2-го порядка, допускающие понижение порядка:
а) 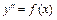 решается повторным интегрированием.
решается повторным интегрированием.
б) 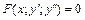 , явно не содержащее искомой функции
, явно не содержащее искомой функции 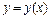 . Используется замена:
. Используется замена: 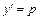 , где
, где 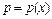 – новая неизвестная функция, тогда
– новая неизвестная функция, тогда 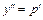 . Для нового уравнения относительно функции p находим общее решение и подставляем его в формулу
. Для нового уравнения относительно функции p находим общее решение и подставляем его в формулу 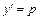 . Получаем ДУ с разделяющимися переменными относительно функции y, находим его общее решение.
. Получаем ДУ с разделяющимися переменными относительно функции y, находим его общее решение.
в) 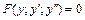 , явно не содержащее независимой переменной
, явно не содержащее независимой переменной 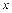 . Замена:
. Замена: 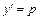 , где
, где 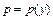 , тогда
, тогда 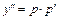 . Для нового уравнения относительно функции p находим общее решение и подставляем его в формулу
. Для нового уравнения относительно функции p находим общее решение и подставляем его в формулу 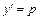 . Получаем ДУ с разделяющимися переменными относительно функции y, находим его общее решение.
. Получаем ДУ с разделяющимися переменными относительно функции y, находим его общее решение.
18. Линейным однородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами называется уравнение вида 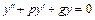 . Составляется характеристическое уравнение
. Составляется характеристическое уравнение 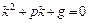 .
.
Если 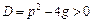 , то
, то 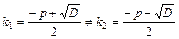 и общее решение исходного уравнения имеет вид:
и общее решение исходного уравнения имеет вид: 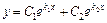 .
.
Если 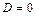 , то
, то 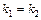 и
и 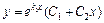 .
.
Если 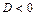 , то
, то 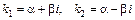 и
и 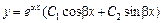 .
.
19. Линейным неоднородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами с правой частью специального вида называется уравнение вида  . Его общее решение ищется в виде
. Его общее решение ищется в виде  , где
, где 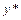 – общее решение соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами:
– общее решение соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами: 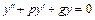 , а
, а 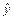 – какое-либо частное решение исходного уравнения.
– какое-либо частное решение исходного уравнения.
Если 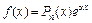 , где a – некоторое число, Pn (x) – многочлен степени n, то
, где a – некоторое число, Pn (x) – многочлен степени n, то 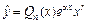 , где
, где 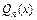 – многочлен степени
– многочлен степени 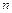 с неопределенными коэффициентами,
с неопределенными коэффициентами, 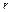 – число, равное кратности a как корня характеристического уравнения
– число, равное кратности a как корня характеристического уравнения 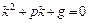 соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами
соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами 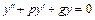 .
.
Если 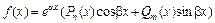 , где a, b – некоторые числа, Pn (x), Qm (x) – многочлены степени n и m соответственно, то
, где a, b – некоторые числа, Pn (x), Qm (x) – многочлены степени n и m соответственно, то 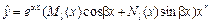 , где
, где 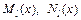 – многочлены степени
– многочлены степени 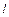 с неопределенными коэффициентами,
с неопределенными коэффициентами, 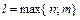 ,
, 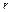 – число, равное кратности
– число, равное кратности 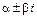 как корня характеристического уравнения
как корня характеристического уравнения 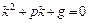 соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами
соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами 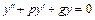 .
.
|
|
Дата добавления: 2014-11-29; Просмотров: 488; Нарушение авторских прав?; Мы поможем в написании вашей работы!