Линейные пространства

ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА

Пусть М - множество, V_m - система подмножеств множест­ва М.

Система V_m называется топологией в М и имеет следующие свойства:

1. М Î V_m; I Î V_m; 2. " (G_i Ç G_k) Î V_m; 3. " (È G_i) Î V_m.

Пример

Рассмотрим топологию базовых множеств: М = {Г;П;В}: Г - группа; П – пространство; В - время.

Топология для базирования объектов определяется множе­ством суммой множеств М.

Множества, принадлежащие системе V_m, называются от­крытыми множествами пространства (М; V_m).

Одно и то же М может порождать ряд топологий, а следо­вательно, и топологических пространств:

,

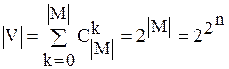V = Æ - отсутствие топологии.

Тривиальная топология - пространство слипшихся точек.

Дискретная топология, если открыто любое подмножество М.

Введем математические объекты: S - множество векторов: х,y,z....; К - множество скаляров:l, m, e..;

Линейное пространство S над полем К определяется как система:

Р = (S, К;j, h),

где j: S ´ S ® S- внутренний закон композиции (аддитивный), S образует абелеву группу, т.е. коммутативную, ассоциативную, с нейтральным (нулевым) и обратным (-х) элемен­тами;

h: K ´ S ® S - внешний закон композиции со свойствами:

а) дистрибутивности относительно внутреннего закона сло­жения векторов: l(х + у) = lx + ly;

б) дистрибутивности относительно аддитивного закона поля К (сложения скаляров): (l + m)x = lx + mх,

в) ассоциативности относительно мультипликативного за­кона поля К: (lm)x = (lx)m;

г) наличие нейтрального элемента (e) относительно умно­жения в поле К: ex = x.

Линейные пространства S над полем К могут быть действи­тельными или комплексными, если К соответственно поле дейст­вительных или комплексных чисел.

Примеры

1. 3-мерные векторы х(х₁;х₂;х₃) образуют действительное линейное пространство j: х + у = z; h:lx.

2. Если S = К, то любое поле К можно рассматривать как векторное пространство над самим собой: j: (+); h:(*).

3. S = {а, b, c}; j: S ´ S ® S; j º (+).

j	a	b	c
a	b	c	a
b	c	a	b
c	a	b	c

Здесь С - нейтральный элемент. Структура типа "абелева группа".

Постройте граф отношения для заданного j.

4. S = {а, b, с), К = {1, 2, 3} - имеем поле вычетов по модулю .

Поле вычетов можно задать в виде таблиц отношений:

*	a	b	c	(+)				(*)
	c	c	c
	a	b	c
	b	a	c
K ´ S ® S	K ´ K ® K

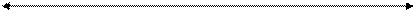
Дата добавления: 2014-12-07