
- Р Р‡.МессенРТвЂВВВВВВВВжер
- ВКонтакте
- РћРТвЂВВВВВВВВнокласснРСвЂВВВВВВВВРєРСвЂВВВВВВВВ
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВВВВВВВРЎР‚
- LiveJournal
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Угловая скорость и угловое ускорение
|
|
|
|
ВОКРУГ НЕПОДВИЖНОЙ ОСИ.
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
Вращательным движением твердого тела вокруг неподвижной оси называется движение твердого тела, имеющего две неподвижные точки (А и В). Прямая OZ, проходящая через эти точки, называется осью вращения.
Для определения положения вращающегося тела возьмем две полу-плоскости I и II, ограниченные осью вращения OZ (рис. 2.3).
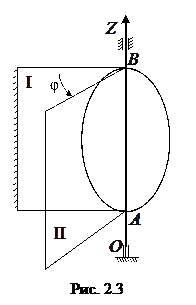 Полуплоскость I неподвижная, а полуплос-кость II врезана в тело и вращается вместе с ним. Тогда положение тела в произвольный момент времени t определяют заданием линейного угла
Полуплоскость I неподвижная, а полуплос-кость II врезана в тело и вращается вместе с ним. Тогда положение тела в произвольный момент времени t определяют заданием линейного угла  двухгранного угла между этими полуплоскостями:
двухгранного угла между этими полуплоскостями:
 . (2.4)
. (2.4)
Угол  называется углом поворота тела. Уравнение (2.4) определяет закон вращательного движения твердого тела вокруг неподвижной оси.
называется углом поворота тела. Уравнение (2.4) определяет закон вращательного движения твердого тела вокруг неподвижной оси.
За положительное направление отсчета угла  выбрано направление против хода часовой стрелки. В системе СИ угол
выбрано направление против хода часовой стрелки. В системе СИ угол  измеряется в радианах.
измеряется в радианах.
Основными кинематическими характе-ристиками вращательного движения твердого тела являются угловая скорость и угловое ускорение.
 Пусть за промежуток времени
Пусть за промежуток времени  тело повернется вокруг оси OZ на угол
тело повернется вокруг оси OZ на угол 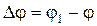 . Угловой скоростью тела в данный момент времени t называется скалярная величина
. Угловой скоростью тела в данный момент времени t называется скалярная величина
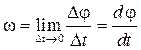 ,
,
 . (2.5)
. (2.5)
Числовое значение угло-вой скорости равно первой производной от угла поворота тела по времени.
Угловая скорость харак-теризует изменение угла пово-рота тела в единицу времени. Угловая скорость измеряется в рад/с или 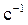 .
.
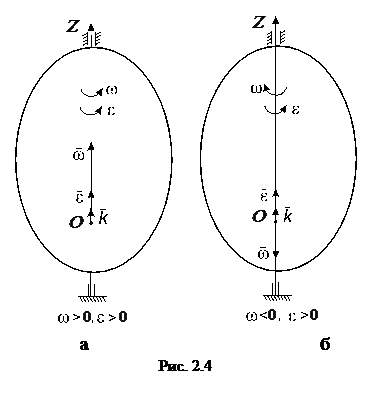
Знак в (2.5) определяет направление вращения тела. Если  , то вращение вокруг оси OZ происходит против хода часовой стрелки (рис. 2.4, а), а если
, то вращение вокруг оси OZ происходит против хода часовой стрелки (рис. 2.4, а), а если 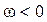 , тогда по ходу часовой стрелки (рис. 2.4, б).
, тогда по ходу часовой стрелки (рис. 2.4, б).
Угловую скорость можно изобразить в виде вектора, направленного по оси вращения:
 , (2.6)
, (2.6)
где  - орт оси OZ. Вектор
- орт оси OZ. Вектор  направлен вдоль оси OZ, если
направлен вдоль оси OZ, если 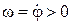 , и против оси OZ, если
, и против оси OZ, если  , т. е. с конца вектора
, т. е. с конца вектора  вращение вокруг оси всегда видно происходящим против хода часовой стрелки (рис. 2.4).
вращение вокруг оси всегда видно происходящим против хода часовой стрелки (рис. 2.4).
Если за время  угловая скорость изменилась на величину
угловая скорость изменилась на величину 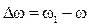 , то угловым ускорением тела в данный момент времени t называется величина
, то угловым ускорением тела в данный момент времени t называется величина 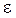 , определяемая выражением
, определяемая выражением

или
 . (2.7)
. (2.7)
Числовое значение углового ускорения тела равно первой производной от угловой скорости или второй производной от угла поворота тела по времени.
Угловое ускорение  характеризует изменение угловой скорости
характеризует изменение угловой скорости 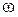 тела в единицу времени. В качестве единицы измерения
тела в единицу времени. В качестве единицы измерения  обычно исполь-зуется рад/c2 или с-2.
обычно исполь-зуется рад/c2 или с-2.
Угловое ускорение тела можно изобразить в виде вектора 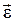 , направ-ленного по оси вращения OZ:
, направ-ленного по оси вращения OZ:
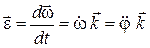 . (2.8)
. (2.8)
Если величина угловой скорости с течением времени возрастает, то вращение тела является ускоренным. В этом случае векторы  и
и  направлены в одну сторону, а их числовые значения имеют одинаковые знаки (или
направлены в одну сторону, а их числовые значения имеют одинаковые знаки (или  (рис. 2.4, а), или
(рис. 2.4, а), или  ).
).
Если величина угловой скорости с течением времени уменьшается, то вращение тела является замедленным. Векторы  и
и  направлены по оси вращения в противоположные стороны, а их числовые значения имеют противоположные знаки (
направлены по оси вращения в противоположные стороны, а их числовые значения имеют противоположные знаки (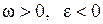 , или
, или  (рис. 2.4, б)).
(рис. 2.4, б)).
Равномерное вращение. Если угловая скорость тела остается во время движения постоянной, то вращение тела называется равномерным. Найдем закон равномерного вращения. Пусть при t = 0  ,
,  . Согласно (2.5) запишем
. Согласно (2.5) запишем 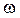 в дифференциальной форме
в дифференциальной форме
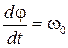
или
 .
.
Возьмём от обеих частей этого равенства определенные интегралы, у которых нижние пределы соответствуют начальным условиям движения, а верхние - произвольному моменту времени t:
 .
.
Отсюда следует закон равномерного вращения:
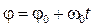 . (2.9)
. (2.9)
Равнопеременное вращение. Если угловое ускорение при движении тела остается постоянным по величине (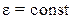 ), то вращение называется равнопеременным. Найдем закон равнопеременного вращения. Пусть при
), то вращение называется равнопеременным. Найдем закон равнопеременного вращения. Пусть при  . Согласно (2.7) запишем
. Согласно (2.7) запишем 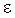 в дифференциаль-ной форме
в дифференциаль-ной форме
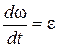
или, разделяя переменные,
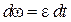 .
.
Интегрируя, получим
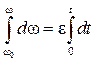 ,
,
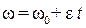
или
 . (2.10)
. (2.10)
Формула (2.10) выражает зависимость угловой скорости от времени при равнопеременном вращении твердого тела. Знак «+» соответствует равноускоренному, а знак «-» - равнозамедленному вращениям. Восполь-зовавшись (2.5), представим (2.10) в виде
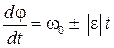 ,
,
или
 .
.
Интегрируя данное уравнение с учетом начальных условий движения
 ,
,
получим закон равнопеременного вращения
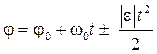 . (2.11)
. (2.11)
Знак «+» в (2.11) соответствует равноускоренному, а знак «-» - равнозамед-ленному вращениям.
|
|
|
Дата добавления: 2014-12-07; Просмотров: 795; Нарушение авторских прав?; Мы поможем в написании вашей работы!