Определение и основное свойство плоскопараллельного движения

Плоскопараллельное движение твердого тела.

УРЕАМИКОПЛАЗМОЗ

Уреамикоплазмоз – заболевание, вызываемое уреаплазмами (Ureaplasma Urealyticum) и микоплазмами (Mycoplasma genitalium и Mycoplasma hominis)/

Клиническая картина микоплазмоза и уреаплазмоза такая же, как и хламидиоза.

Лечение:

F антибиотики – тетрациклины;

F иммуностимуляторы;

F физиотерапия: грязелечение, парафинолечение, индуктотермия, лазеротерапия и др.;

F местное лечение антисептиками.

Задание движения .

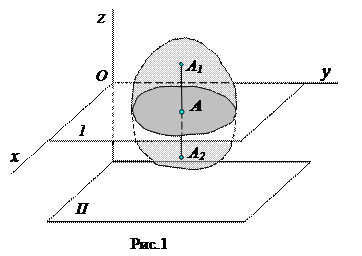Плоскопараллельным называется такое движение твердого тела (рис.1), при котором траектории всех его точек лежат в плоскостях, параллельных одной и той же неподвижной плоскости.

Неподвижная плоскость называетсяосновной.

Примером плоскопараллельного движения может служить движение цилиндра по горизонтальной плоскости, при котором его основание остается параллельным вертикальной плоскости (рис.2).

Основная теорема плоскопараллельного движения.

Все точки тела, лежащие на общем перпендикуляре к основной плоскости, движутся по одинаковым траекториям и имеют геометрически равные скорости и ускорения. Такими точками (рис.1) являются точки А, А₁, и А₂.

Сформулированное свойство является следствием определения плоскопараллельного движения. Действительно, из определений плоскопараллельного движения и твердого тела следует, что углы между любыми прямыми, фиксированными в твердом теле, сохраняются неизменными. Следовательно любая прямая А₁А₂, проведенная в теле, перпендикулярно основной плоскости П, будет перемещаться поступательно, т.е. траектории, скорости и ускорения всех точек этой прямой будут одинаковыми.

Таким образом, для определения движения тела необходимо знать движение лишь одной точки каждой прямой, проведенной перпендикулярно плоскости П, т.е. точки, лежащие в одной плоскости 1, параллельной основной плоскости, определяют плоскопараллельное движение твердого тела.

Плоскопараллельное движение твердого тела полностью характеризуется движением плоской фигуры в своей плоскости. Плоская фигура (рис.1) получается сечением твердого тела плоскостью 1, параллельной основной плоскости П. Движение плоской фигуры в своей плоскости называется плоским.

Задание плоского движения

Рассмотрим движение плоской фигуры в своей плоскости. Положение плоской фигуры в своей плоскости определяется положением двух ее точек.

Пусть точки (рис.3) А (х_А,у_А) и В (х_В, у_В) – две точки плоской фигуры, движущейся в плоскости Оху. Так как расстояние между этими точками остается постоянным

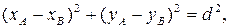
то из четырех координат, определяющих положение этих точек, независимых остается только три.

Таким образом, для описания плоского движения требуется знать три независимых параметра.

Свяжем жестко с плоской фигурой систему координат Ах₁у₁ (рис.4). Тогда положение системы Ах₁у₁, а вместе с ней и положение плоской фигуры относительно системы координат Оху будет определено заданием координат х_А,у_А точки А и углом между φ между осями Ах₁ и Ах₂ (рис.4).

Следовательно, положение плоской фигуры в своей плоскости в любой момент времени полностью определяется тремя функциями времени

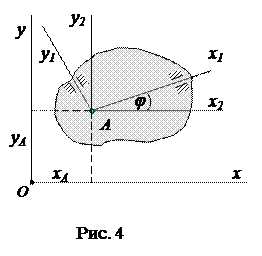
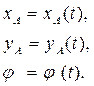(1)

Уравнения (1) называются уравнениями движения плоской фигуры или уравнениями плоскопараллельного движения твердого тела.

Первые два уравнения (рис.3) определяют положение выбранного полюса А на плоскости, последнее - угол поворота вокруг этого полюса.

Дата добавления: 2014-12-07