Ускорения точек плоской фигуры

Кривошип и шатун расположены на одной прямой (рис.19).

Пример. Кривошипно-шатунный механизм

Угловая скорость кривошипа равна ω_ОА. Определить угловую скорость шатуна и скорости точек А,В, и С для трех положений механизма.

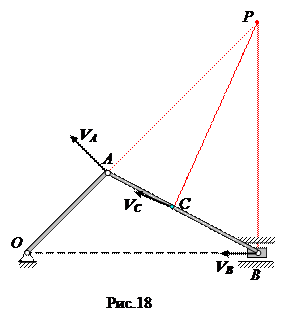Кривошип ОА вращается вокруг точки О, шатун АВ совершает плоское движение в плоскости чертежа. Во всех случаях скорость точки А перпендикулярна кривошипу и равна , а скорость точки В направлена по горизонтальной прямой.

1. Кривошип ОА образует острый угол с горизонтальной прямой (рис.18). В этом случае мгновенный центр скоростей шатуна находится в точке Р, где пересекаются восстановленные в точках А и В перпендикуляры к скоростям в этих точках.

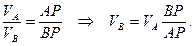
Скорость точки С направлена перпендикулярно отрезку РС и находится из пропорции:

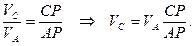
Угловая скорость шатуна равна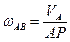

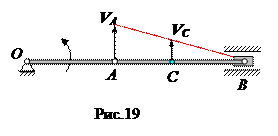В этом положении мгновенный центр скоростей находится в точке В, поэтому скорость V_B равна нулю. Скорость точки С находится из пропорции:

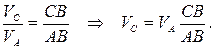
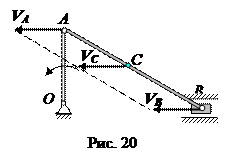Угловая скорость шатуна равна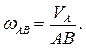

3. Кривошип занимает вертикальное положение (рис.20). В этом случае мгновенный центр скоростей шатуна находится в бесконечности, скорости всех его точек равны, угловая скорость шатуна равна нулю.

Пример1

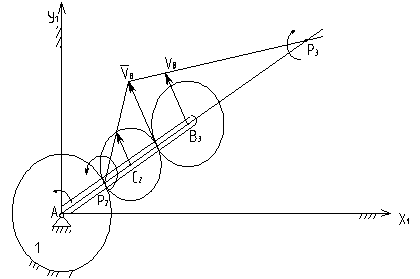Известны радиусы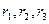

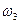шестерей и угловая скорость

криволинейна AB ,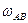

Найти угловую скорость 3

Колеса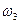

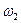
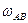
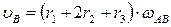
Найти скорость K, как точки сцепления 2 и 3.

Для шестерни 2:

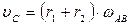
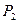- мгновенный центр скоростей шестерен

2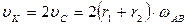

Тогда,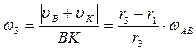

Когда,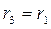

Движение плоской фигуры в своей плоскости можно разложить на поступательное движение вместе с произвольно выбранной точкой, принимаемой за полюс, и вращательное движение вокруг этого полюса.

Следовательно, ускорение любой точки при плоском движении равно геометрической сумме двух ускорений: ускорения выбранного полюса, и ускорения, полученного данной точкой при ее вращательном движении вокруг полюса.

Пусть известно ускорение точки А плоской фигуры, тогда ускорение другой точки этой фигуры будет равно

,

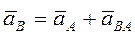где ускорение вращательного движения точки А вокруг точки В раскладывается на нормальное и касательное ускорения:

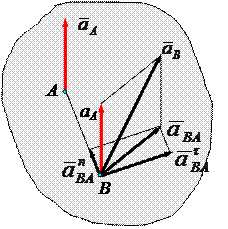
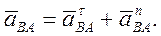
Касательное ускорение вращательного движения точки вокруг полюса направлено перпендикулярно отрезку АВ, соединяющему точку В с полюсом А, и равно

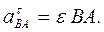
Нормальное ускорение направлено по отрезку ВА к полюсу А и равно

Окончательно, полное ускорение точки В равно геометрической сумме трех ускорений: ускорения выбранного полюса А, нормального и касательного ускорений вращательного движения точки В вокруг этого полюса:

.

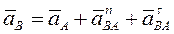Мгновенным центром ускорений называется точка, принадлежащая связанной с плоской фигурой плоскости, ускорение которой в данный момент равно нулю. Если за полюс выбрать мгновенный центр ускорений, то ускорение произвольной точки плоской фигуры определяется как ускорение вращательного движения вокруг мгновенного центра ускорений.

,

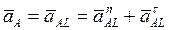где L –мгновенный центр ускорений, 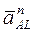- нормальное ускорение, 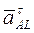- касательное ускорение точки А вращательного движения плоской фигуры вокруг мгновенного центра ускорений.

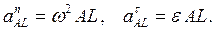
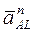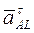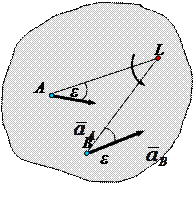
Ускорение - направлено по AL, ускорение - перпендикулярно AL. Ускорение 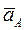точки А образует угол α с отрезком AL соединяющим точку А с мгновенным центром ускорений и равно (рис.12)

,

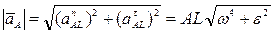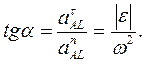
Таким образом, если известно ускорение точки А плоской фигуры, то, чтобы найти положение мгновенного центра ускорений, следует это ускорение повернуть вокруг точки А на угол α в сторону вращения фигуры и на полученной прямой отложить расстояние

.

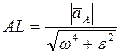Если известны направления ускорений двух точек плоской фигуры, то мгновенный центр ускорений определяется как точка пересечения полученных поворотом этих ускорений на один и тот же угол 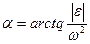в сторону вращения.

Пример. Центр колеса, катящегося без скольжения по горизонтальной плоскости, в данный момент имеет скорость V_C = 2 м/c и ускорение а_C = 1,6 м/c. Радиус колеса R = 0,4 м. Определить ускорение точек В и Р (рис.40).

Так как скорость и ускорение точки С известны, то принимаем точку С за полюс.

Тогда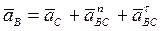

,

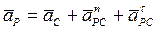где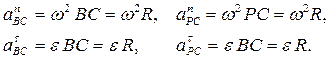

Мгновенный центр скоростей колеса находится в точке Р – точке касания колеса с неподвижной плоскостью, поэтому

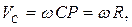откуда 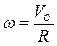, при t = 1c, ω =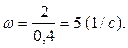

Угловое ускорение колеса

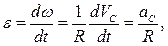при t =1 c,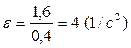

Тогда .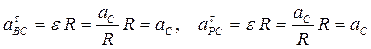

Ускорение точки Р будет направлено к центру колеса точке С и равно

.

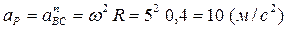Для определения ускорения в точке В спроектируем векторное равенство 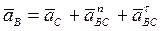на горизонтальную ось x и вертикальную ось у:

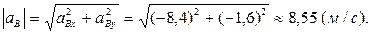
Лекция №8

Дата добавления: 2014-12-07