Ускорение точки тела

Скорость и ускорение точки при сферическом движении твердого тела

Перемещаясь в пространстве и внутри тела, Мгновенная ось опишет собой конические поверхности, которые называются соответственно неподвижным и подвижным аксоидами. Для получения уравнений этих поверхностей необходимо из уравнений мгновенной оси вращения исключить время.

Подвижный аксоид катится без проскальзывания по неподвижному. Данный вывод следует из равенства нулю скоростей точек мгновенной оси вращения, которая является в текущий момент общей для неподвижного и подвижного аксоидов.

Ускорение произвольной точки тела может быть определено по формуле Ривальса:

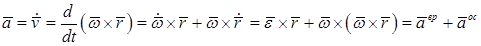
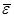где — вращательное ускорение, направленное перпендикулярно к векторам и 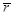; 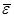— угловое ускорение тела, совершающего сферическое движение.

Вектор углового ускорения направлен вдоль мгновенной оси ускорений, которая определяется из условия равенства нулю вращательного ускорения произвольной точки оси ускорений;

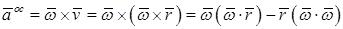— осестремительное ускорение, перпендикулярное векторам 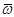и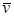

Задача №1

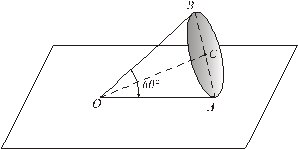
Конус с углом при вершине 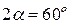и радиусом основания 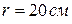катится по неподвижной горизонтальной плоскости без скольжения. Скорость центра основания 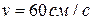постоянна.

Определить:

1. угловую скорость конуса ;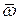

2. угловое ускорение конуса ;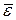

3. скорости наинизшей и наивысшей точек основания А и В ;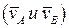

4. ускорение этих точек .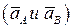

Решение:

1) Определяем 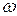угловую скорость конуса. ОР - мгновенная ось вращения.

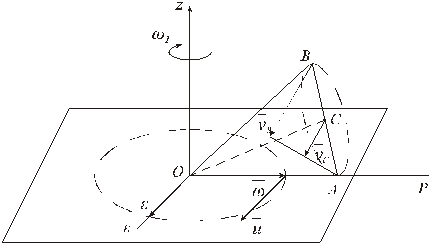
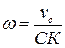
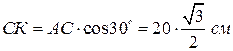
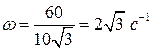
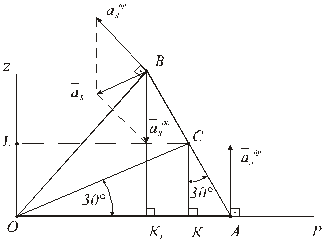
2) Определяем угловое ускорение тела.

Для определения углового ускорения 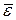необходимо построить годограф угловой скорости 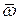. Вектор 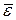геометрически равен скорости 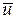конца вектора 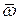. В данном случае скорость 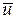является вращательной вокруг оси OZ. Угловая скорость этого вращения 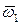определяется как угловая скорость вращения оси ОС вокруг оси OZ.

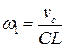
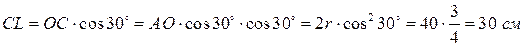
Скорость 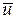находим как вращательную скорость вектора угловой скорости 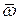- при вращении вокруг оси OZ.

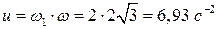
т.е.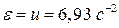

3) Определим скорости точек тела:

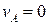, т.к. точка А лежит на мгновенной оси вращения

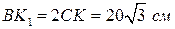
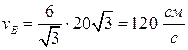
4) Определяем ускорения точек тела.

Ускорение точки тела определяем как геометрическую сумму осестремительного ускорения 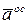во вращении тела вокруг мгновенной оси ОР и вращательного 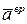относительно оси углового ускорения .

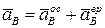
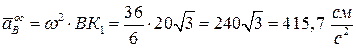
Для определения вращательного ускорения опускаем из точки В перпендикуляр на ось углового ускорения, который совпадает с отрезком

в плоскости POZ

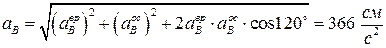
В точке А, лежащей на мгновенной оси вращения, осестремительное ускорение равно нулю:

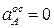
Определяем модуль вращательного ускорения точки А:

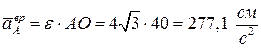
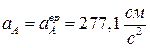
Дата добавления: 2014-12-07