
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Статистические оценки параметров распределения
|
|
|
|
Изучаемую совокупность можно считать выборкой из генеральной совокупности, состоящей из большого множества сельскохозяйственных предприятий. На основе показателей, рассчитанных по выборке, дают статистическую оценку параметров генеральной совокупности.
Статистической оценкой называется специальная функция, вычисляемая на основании выборочных данных для приближенной замены неизвестного параметра распределения или самого распределения. Различают оценки смещённые и несмещённые, точечные и интервальные.
Возможное расхождение между выборочными и генеральными характеристиками составляет ошибку выборки.
Стандартная ошибка выборочной средней определяется по формуле:

Точечной оценкой генеральной средней является выборочная средняя 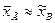 .
.
Для определения интервальной оценки необходимо найти доверительный интервал 
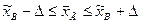 ,
,  ,
,
где 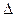 - предельная ошибка выборочной средней;
- предельная ошибка выборочной средней; 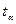 - коэффициент доверия, который определяют по таблице распределения Стьюдента по заданным
- коэффициент доверия, который определяют по таблице распределения Стьюдента по заданным 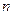 и
и 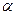 при малой выборке n <= 30 (приложение 4).
при малой выборке n <= 30 (приложение 4).
Для нахождения доверительного интервала в Excel выбираем Статистические функции – Доверит, ОК, в появившемся окне заполняем поля: Альфа - уровень значимости (α = 0,05 или 0,01 для социально-экономических явлений); Стандартное отклонение – среднее квадратическое отклонение; Размер – объём выборки (в нашей работе n=30). Нажимаем ОК, появляется значение функции. Так, для урожайности озимой пшеницы в поле Альфа ставим уровень значимости α = 0,05; в поле Стандартное отклонение – 0,4947, в поле Размер – объём выборки 30. При нажатии ОК видим значение 0,177. Это предельная ошибка выборки, С её помощью строим доверительный интервал для генеральной средней:
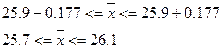
Вывод: с вероятностью 0,95 мы можем утверждать, что генеральная средняя не выйдет за пределы от 25,7 до 26,1 ц/га.
Аналогичные действия выполним для затрат труда на 1 ц зерна. В соответствующие поля введём уровень значимости, среднее квадратическое отклонение, объём выборки: 0,05; 0,04; 30. Щёлкаем ОК и получаем 0,014. Строим доверительный интервал:
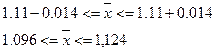
Вывод: с вероятностью 0,95 можно утверждать, что средние затраты труда на 1 ц зерна находятся в интервале от 1,096 до 1,124 чел.-ч.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 324; Нарушение авторских прав?; Мы поможем в написании вашей работы!