Проверка гипотезы о законе нормального распределения

Для объективной оценки степени соответствия эмпирического распределения теоретическому используется ряд особых показателей, называемых критериями согласия. На их базе проверяется гипотеза о законе нормального распределения. Это критерии Пирсона, Колмогорова, Романовского, Смирнова и др. Мы рассмотрим критерий Пирсона.

Критерий Пирсона (хи-квадрат) определяется по формуле:

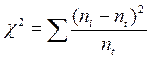,(1)

где (хи-квадрат) – критерий Пирсона; n_i – эмпирические частоты; n_t – теоретические частоты.

Теоретические частоты вычисляются по формуле:

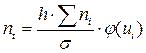,(2)

где 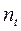– теоретические частоты; 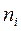- фактические частоты; 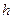- шаг (величина интервала); - нормированные отклонения; 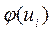- значения функции плотности стандартизированного нормального распределения (даны в приложении 2).

Вычисления выполняются в следующей последовательности.

1)Определяются 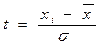нормированные отклонения:

(3)

2)При рассчитанных значениях t по таблице плотности нормального распределения (значений дифференциальной функции

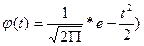отыскиваются значения функции плотности стандартизированного нормального распределения.

3)Вычисляется выражение .

4)По приведённой выше формуле (1) рассчитывается критерий Пирсона.

4)Подставляя в формулу значения φ(t) и , определяют теоретические частоты.

Рассчитанное значение критерия сравнивается с табличным при соответствующем числе степени свободы и заданном уровне значимости. Если расчетное значение χ² меньше табличного, то делается вывод о несущественности расхождений между эмпирическим и теоретическим распределением (т.е. нулевая гипотеза о том, что распределение подчиняется закону нормального распределения, принимается). В противном случае утверждается, что исследуемое эмпирическое распределение имеет отличный от теоретического закон распределения.

Возможен вариант проверки гипотезы соответствия эмпирического распределения теоретическому с помощью таблиц определения вероятности Р(χ²). В таблице распределения Пирсона (приложение 9) по рассчитанной величине χ² и числу степеней свободы ν=к-1 находим вероятность Р(χ²). При Р>0.5 считается, что эмпирическое и теоретическое распределения близки. В остальных случаях делается вывод о несовпадении эмпирического и теоретического распределений.

3.7.Проверка гипотезы о законе нормального распределения по критерию Пирсона с помощью табличного процессора Excel

Вместо заполнения большого количества таблиц можно воспользоваться статистическими функциями.

Проверку гипотезы о законе нормального распределения выполним на примере интервального вариационного ряда, построенного в пункте 2.2, и статистических характеристик ряда из пункта 3.4.

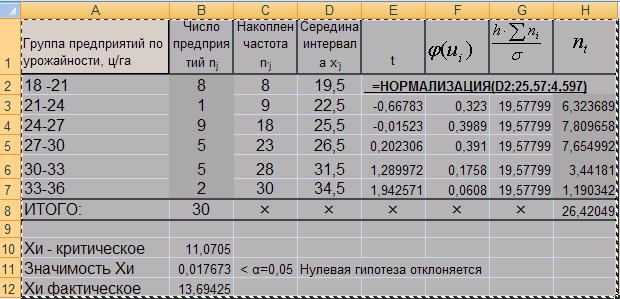
Рис. 3. Хи тест

1. Находим нормализованные значения признака (рис 1.). Вызываем список функций, выбираем функцию «НОРМАЛИЗАЦИЯ» (STANDATRDIZE). В поле «Х» вводим название ячейки первого интервала, во втором поле среднее значение по выборке, в третьем поле стандартное отклонение выборки. Копируем данную формулу для остальных строк.

2. По таблице плотности распределения φ(u) находим вероятность распределения этих значений и заполняем следующий столбец.

3. Следующий столбец заполняем рассчитанным выражением .

4. Находим теоретические частоты по формуле (2) и заполняем последний 8 столбец.

5. Далее, для вычисления критерия Пирсона, воспользуемся функцией «ХИ2ТЕСТ». В поле «Фактический интервал» выделяем массив фактических частот, в поле «Ожидаемый интервал» вводим массив теоретических частот. В результате получаем значимость фактического критерия Пирсона. Чтобы получить фактическое значение критерия Пирсона, воспользуемся функцией «ХИ2ОБР». В поле «вероятность» вводим полученную значимость критерия (ячейка B11), а в поле «степени_свободы» соответствующее число степеней свободы для данной группировки. В данном случае n-1=5 (n – число групп).

Полученную в пункте 5 фактическую значимость критерия Пирсона «p» сравниваем с установленным уровнем значимости «α». Если α_факт <α= 0,05, то утверждаем, что эмпирическое распределение сходно с теоретическим и нулевая гипотеза отвергается. Далее, если нужно, мы находим фактическое значение критерия по значимости «α » и числа степеней свободы.

4.Корреляционно-регрессионный анализ

4.1.Определение параметров уравнения регрессии и показателей тесноты корреляционной связи

Социально-экономические явления находятся между собой в сложной взаимосвязи, зависимости. По характеру зависимости статистика различает два вида связей:

1)функциональную;

2)корреляционную.

Корреляционная связь характеризуется тем, что между изменением независимой переменной (факторного признака) и зависимой переменной нет полного соответствия: каждому значению факторного признака может соответствовать распределение значений результативного.

Корреляционная связь проявляется лишь в массе случаев – в совокупности достаточно большого объема. При этом изменение независимой величины ведет к изменению среднего значения зависимой переменной.

По направлению различают прямые и обратные связи. При прямой связи с увеличением факторного признака увеличивается результативный. При обратной связи с ростом факторного признака значения результативного уменьшаются.

По аналитическому выражению связи делятся на прямолинейные (линейные) и криволинейные (нелинейные). Линейная связь выражается линейной функцией (уравнением прямой), нелинейная – криволинейной в виде параболы, гиперболы, показательной кривой и т.д.

Функция, отображающая корреляционную связь между признаками, называется уравнением регрессии. Уравнение регрессии выражается функцией у = f(х1,х2,…, хn).

Уравнения регрессии могут иметь следующую форму.

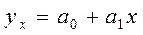
Уравнение прямой:

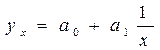Уравнение гиперболы:

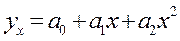Уравнение параболы второго порядка:

Степенное уравнение:

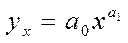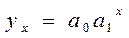Показательное уравнение

Многофакторная корреляционная связь чаще всего описывается линейным уравнением множественной регрессии:

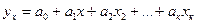
Параметр α₁ в уравнении прямой называется коэффициентом регрессии. Он показывает, на сколько в среднем изменяется величина результативного признака при изменении факторного на единицу. При прямой корреляционной связи коэффициент регрессии имеет положительный знак, при обратной – отрицательный.

Количественная характеристика корреляционной связи дается с помощью ряда статистических показателей – коэффициентов корреляции, регрессии и т.д.

Наиболее распространенным и совершенным методом изучения корреляционных связей является корреляционно-регрессионный анализ.

В процессе корреляционно-регрессионного анализа (КРА) решаются следующие задачи:

1) определение формы и направления связи, ее количественное выражение в виде уравнения регрессии;

2) характеристика тесноты связи.

3) определение значимости, существенности выборочных характеристик тесноты корреляционной связи;

Параметры уравнения регрессии находятся способом наименьших квадратов. Сущность метода заключается в нахождении параметров уравнения, при которых сумма квадратов отклонений фактических значений результативного признака от теоретических, полученных по выбранному уравнению регрессии, минимальна. Он дает систему нормальных уравнений, решая которую определяют параметры уравнения регрессии.

Для уравнения парной линейной регрессии у_х=α₀+α₁х система нормальных уравнений следующая: следующая::

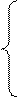Для гиперболы:

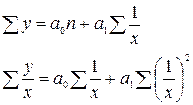Для параболы второго порядка:

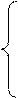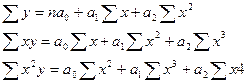Параметры уравнения множественной регрессии при большом числе факторов рассчитываются на ЭВМ.

Для характеристики тесноты парной корреляционной связи используются в основном два показателя:

· линейный коэффициент корреляции и соответствующий ему коэффициент детерминации;

· корреляционное отношение и соответствующий ему индекс детерминации.

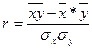Для измерения тесноты парной линейной связи вычисляется линейный коэффициент корреляции. Статистика разработала ряд формул линейного коэффициента корреляции:

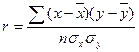где σ_х- среднее квадратическое отклонение по факторному признаку;

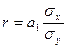σ_у – среднее квадратическое отклонение по результативному признаку.

Линейный коэффициент корреляции может принимать значения от минус единицы до плюс единицы. Положительный коэффициент корреляции указывает на прямую корреляционную связь, отрицательный – на обратную. Знак при коэффициенте корреляции совпадает со знаком коэффициента регрессии. Принята следующая условная градация коэффициента корреляции: r<0,3 – связь слабая, r=0,3 – 0.7 – связь средней силы, r>0.7 – связь тесная.

Квадрат коэффициента корреляции носит название коэффициента детерминации. Он показывает долю факторного признака в вариации результативного.

Коэффициент корреляции достаточно точно оценивает степень тесноты связи лишь при линейной форме зависимости. Для характеристики тесноты связи любой формы используется корреляционное отношение. Теоретическое корреляционное отношение определяется по формуле:

где δ² – факторная дисперсия – дисперсия теоретических значений результативного признака, т.е. рассчитанных по уравнению регрессии;

σ² – дисперсия эмпирических (фактических) значений результативного признака.

Указанные дисперсии исчисляются по формулам:

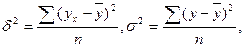
где у_х – теоретические значения результативного признака;

ỹ - среднее значение результативного признака в совокупности;

у – фактические (эмпирические) значения результативного признака.

При линейной связи корреляционное отношение и коэффициент корреляции равны.

Корреляционное отношение может принимать значения от нуля до единицы. Чем ближе данный показатель к единице, тем теснее связь между изучаемыми признаками.

Параметры уравнения регрессии и коэффициент корреляции могут быть рассчитаны с помощью табличного процессора Excel. Для этого на лист Excel копируем исходные данные. В меню Сервис выберем опцию Анализ данных. Щелкнув левой кнопкой мыши по этому пункту, откроем инструмент Регрессия. Щелкаем по кнопке OK, на экране появляется диалоговое окно Регрессия. В поле Входной интервал У вводим значения результативного признака, в поле Входной интервал Х вводим значения факторных признаков. Отмечаем уровень вероятности 95%, выбираем Новый рабочий лист. Щелкаем по кнопке OK. На рабочем листе появляются результаты вычисления параметров уравнения регрессии, коэффициента корреляции и другие показатели, позволяющие определить значимость коэффициента корреляции и параметров уравнения регрессии.

Дата добавления: 2014-12-07