
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обчислення дисперсії для 7-Б кл
|
|
|
|
Обчислення дисперсії для 7-А кл.
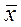   Кількість правильно виконаних тестових завдань з біології, хі Кількість правильно виконаних тестових завдань з біології, хі
| Частота оцінок, f | хі – 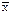
| (хі – 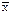 )2 )2
| f· (хі – 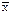 )2 )2
| |
| -2,81 | 7,70 | 15,4 | |||
| -1,81 | 3,28 | 13,12 | |||
| -0,81 | 0,66 | 4,62 | |||
| 0,19 | 0,04 | 0,32 | |||
| 1,19 | 1,42 | 8,52 | |||
| 2,19 | 4,80 | 14,4 | |||
| 3,19 | 10,18 | 10,18 | |||
| N = 31 | 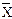 = 7,81 = 7,81
| Σ = 98,24 | |||
| σ12 = 3,17 | |||||
Таблиця2.8
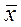 Кількість правильно виконаних
завдань з біології, хі Кількість правильно виконаних
завдань з біології, хі
| Частота оцінок, f | хі – 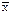
| (хі – 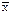 )2 )2
| f· (хі – 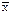 )2 )2
|
| -2,69 | 7,24 | 7,24 | ||
| -1,69 | 2,86 | 11,44 | ||
| -0,69 | 0,48 | 2,40 | ||
| 0,31 | 0,10 | 0,90 | ||
| 1,31 | 1,72 | 12,04 | ||
| 2,31 | 5,34 | 10,68 | ||
| 3,31 | 11,00 | 11,00 | ||
| N = 29 | 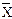 = 7,69 = 7,69
| Σ = 55,7 | ||
| σ22 = 1,92 |
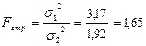
Потім знаходимо в F-таблиці (табл. 2.9), значення Fkrit. В головці таблиці шукають значення сукупності з більшою дисперсією (σ12), а в боковику – з меншою дисперсією (σ22). Якщо Femp > Fkrit, то вибірки суттєво різняться, якщо Femp ≤ Fkrit, то вибірки схожі за даною ознакою.
У нашому прикладі Femp < Fkrit (1,65 < 1,70), отже, 7-А і 7-Б класи істотно не відрізняються за своєю успішністю з біології. Вірогідність того, що ці класи, подібні складає 95%.
Таблиця 2.9
Таблиця F-критерію (достовірність 95%)
| Знаменник N2 – 1 | Чисельник N1 – 1 | |||||
| ∞ | ||||||
| 6,4 | 6,3 | 6,2 | 5,9 | 5,8 | 5,6 | |
| 5,2 | 5,1 | 5,0 | 4,7 | 4,5 | 4,4 | |
| 4,5 | 4,4 | 4,3 | 4,0 | 3,8 | 3,7 | |
| 4,1 | 4,0 | 3,9 | 3,6 | 3,4 | 3,2 | |
| 3,8 | 3,7 | 3,6 | 3,3 | 3,1 | 2,9 | |
| 3,6 | 3,5 | 3,4 | 3,1 | 2,9 | 2,7 | |
| 3,5 | 3,3 | 3,2 | 2,9 | 2,7 | 2,5 | |
| 3,4 | 3,2 | 3,1 | 2,8 | 2,6 | 2,4 | |
| 3,3 | 3,1 | 3,0 | 2,7 | 2,5 | 2,3 | |
| 3,2 | 3,0 | 2,9 | 2,6 | 2,4 | 2,2 | |
| 3,1 | 3,0 | 2,9 | 2,5 | 2,3 | 2,1 | |
| 3,1 | 2,9 | 2,8 | 2,5 | 2,3 | 2,1 | |
| 3,0 | 2,9 | 2,7 | 2,4 | 2,2 | 2,0 | |
| 3,0 | 2,8 | 2,7 | 2,4 | 2,2 | 2,0 | |
| 2,9 | 2,8 | 2,7 | 2,3 | 2,1 | 1,9 | |
| 2,9 | 2,7 | 2,6 | 2,3 | 2,1 | 1,9 | |
| 2,9 | 2,7 | 2,6 | 2,3 | 2,1 | 1,8 | |
| 2,8 | 2,7 | 2,6 | 2,2 | 2,0 | 1,8 | |
| 2,8 | 2,6 | 2,5 | 2,2 | 2,0 | 1,7 | |
| 2,7 | 2,6 | 2,5 | 2,2 | 2,0 | 1,7 | |
| 2,7 | 2,6 | 2,4 | 2,1 | 1,9 | 1,7 | |
| 2,7 | 2,5 | 2,4 | 2,1 | 1,9 | 1,6 | |
| 2,6 | 2,5 | 2,3 | 2,0 | 1,8 | 1,5 | |
| 2,5 | 2,4 | 2,3 | 1,9 | 1,7 | 1,4 | |
| 2,5 | 2,3 | 2,2 | 1,8 | 1,6 | 1,3 | |
| ∞ | 2,4 | 2,2 | 2,1 | 1,8 | 1,5 | 1,0 |
N1 – кількість членів І сукупності.
N2 – кількість членів ІІ сукупності.
Якщо Femp > Fkrit, то для більш точної перевірки і встановлення достовірності різниці класів використовується t-критерій, що обчислюється за формулою:
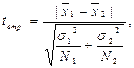 |
{Формула 2.8}
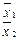 |
де – середнє, арифметичне першої сукупності;
– середнє арифметичне другої сукупності;
N1 – об’єм першої вибірки (кількість членів першої сукупності);
N2 – об’єм другої вибірки (кількість членів другої сукупності);
σ12 – дисперсія першої сукупності;
σ22 – дисперсія другої сукупності.
Після знаходження temp його порівнюють з tkrit, взятим з таблиці 2.10.
Таблиця 2.10
Таблиця t – критерію
| N 1 + N 2 – 2 | Достовірність | |
| 95% | 99% | |
| 12,71 | 63,66 | |
| 4,30 | 9,93 | |
| 3,19 | 5,84 | |
| 2,78 | 4,60 | |
| 2,57 | 4,03 | |
| 2,30 | 3,36 | |
| 2,23 | 3,17 | |
| 2,18 | 3,06 | |
| 2,15 | 2,98 | |
| 2,12 | 2,92 | |
| 2,10 | 2,88 | |
| 2,09 | 2,85 | |
| 2,07 | 2,82 | |
| 2,06 | 2,80 | |
| 2,05 | 2,78 | |
| 2,05 | 2,76 | |
| 2,04 | 2,75 | |
| 2,02 | 2,70 | |
| 2,00 | 2,66 | |
| 1,98 | 2,62 | |
| ∞ | 1,96 | 2,58 |
N1 – кількість членів І сукупності.
N2 – кількість членів ІІ сукупності.
Якщо temp > tkrit, то сукупності різняться за досліджуваною ознакою, вони не однакові (з 95% ймовірністю), якщо temp ≤ tkrit, то відмінності цих вибірок не достовірні, тобто досліджувані групи подібні за певною ознакою і можуть бути використані для подальшого експерименту у ролі контрольних та експериментальних груп.
Непараметричний метод порівняння результатів дослідження – метод χ2
Використовується для обчислення значень, отриманих в результаті вимірювання порядковими та інтервальними шкалами, якщо необхідно встановити чи існує істотна відмінність між рядами показників двох сукупностей. Ґрунтується метод χ2 на порівнянні частот, що характеризують розподіл значень. Метод χ2 або критерій К.Пірсона інакше називають критерієм злагоди.
Для початку слід розбити ряд упорядкованих значень на інтервали. Наприклад, ряд значень семестрових оцінок із біології учнів 6-го класу (табл.2.11) перегрупуємо в інтервали (табл.2.12). При чому, для обчислення χ2-критерію слід перегрупувати інтервали так, щоб сума частот в них була не менше, ніж 4-5 (тобто слід додати інтервали з малими частотами). Нові перегруповані дані заносимо до робочої таблиці обчислення χ2-критерію (табл. 2.12). χ2 обчислюють за формулою:
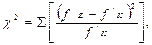 |
{Формула 2.9}
де f/E – відносна частота інтервалу одного ряду (наприклад, експериментального класу);
f/K – відносна частота інтервалу другого ряду (контрольного класу).
Якщо об’єми досліджуваних вибірок однакові (однакова кількість учнів у контрольній та експериментальній групі), то можна не вираховувати відносні частоти. В іншому випадку слід використовувати відносні частоти (у %). Наприклад, в кінці першого семестру 6-А і 6-Б класів з біології розподілились так (див. табл. 2.12).
Таблиця 2.11
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 456; Нарушение авторских прав?; Мы поможем в написании вашей работы!