Методи встановлення зв’язку

Розподіл семестрових оцінок з біології учнів 6-А і 6-Б класів

Семестрова оцінка	Частота оцінок в 6-А кл., f^/E	Частота оцінок в 6-Б кл., f^/К
	∑f^/E = 32	∑f^/E = 32

Таблиця 2.12

Робоча таблиця обчислення х²-критерія

Кількість інтервалів, n	Інтервали оцінок	Частота f^/E	Частота f^/К	f^/E – f^/К	(f^/E – f^/К)^2	(f^/E – f^/К)^2 f^/К
	0-6					0,25
				-2		0,50
				-1		0,11
						0,16
	10-12					0,20
		∑1 = 32	∑1 = 32			χ^2 ≈ 1,22

У нашому прикладі χ² _emp = 1,22. Знаходимо χ² _krit за даними табл.2.13. При чому n – це кількість інтервалів. Для нашого випадку n = 5, χ² _krit = 9,49. Якщо χ² _emp ≤ χ² _krit, то досліджувані вибірки подібні, якщо χ² _emp > χ² _krit, то групи суттєво різняться. Як показали результати дослідження, успішність учнів 6-А і 6-Б класу з біології достатньо схожа і групи подібні за цією ознакою.

Таблиця 2.13

Таблиця χ² – критерію

n – 1	Достовірність
95%	99%
	3,84	6,63
	5,99	9,21
	7,81	11,3
	9,49	13,3
	11,1	15,1
	12,6	16,8
	14,1	18,5
	15,5	20,1
	16,9	21,7
	18,3	23,2
	19,7	24,7
	21,0	26,2
	22,4	27,7
	23,7	29,1
	2,50	30,6
n – кількість інтервалів

Оскільки в педагогічному процесі більшість явищ взаємообумовлені і взаємопов’язані, то дослідникам часто доводиться встановлювати наявність або відсутність такого зв’язку між досліджуваними параметрами, використовуючи коефіцієнти кореляції. Метод кореляції допомагає з високою ймовірністю стверджувати наявність зв'язку між параметрами. Зокрема, так можна встановити залежність успішності учнів з навчального предмету від розвитку їхньої пізнавальної активності чи спостережливості або від рівня розвитку загальнонавчальних умінь. Для інтервальних шкал застосовують лінійну кореляцію (за К. Пірсоном), а для порядкових і невеликих вибірок – порядкову, або рангову, кореляцію (за Спірменом).

Лінійна кореляція (за К.Пірсоном)

Обчислюється коефіцієнт лінійної кореляції (ρ) за формулою:

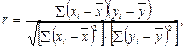
{Формула 2.10}

де (х_i – 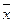) – відхилення кожного окремого значення х від середнього арифметичного ();

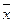(y_i – 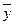) - відхилення кожного окремого значення y від середнього арифметичного ().

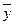Ця ж формула у вигляді більш зручному для підрахунку.

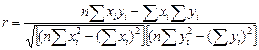{Формула 2.11}

Отриманий емпіричний коефіцієнт лінійної кореляції (r_emp)слід порівняти з його табличним значенням (r_krit) за табл. 2.14, у якій наведені 95% і 1% ймовірності; де n – кількість пар, що порівнюються.

Таблиця 2.14

Таблиця достовірності коефіцієнта лінійної кореляції

n – 2	Достовірність
95%	99%
	0,95	0,99
	0,88	0,96
	0,81	0,92
	0,75	0,87
	0,70	0,83
	0,67	0,80
	0,63	0,77
	0,60	0,74
	0,48	0,61
	0,42	0,53
	0,38	0,49
	0,32	0,42
	0,27	0,35
	0,25	0,33
	0,22	0,28
	0,19	0,25
	0,14	0,18

n – об’єм вибірки (кількість пар, що порівнюються).

Якщо ׀r_emp׀ ≥ r_krit, то існує достовірний зв’язок між двома досліджуваними явищами. При чому чим більша різниця між r_emp і r_krit, тим сильнішим цей зв’язок є. Якщо r_emp має від’ємне значення, то зв’язок між явищами, що досліджуються є оберненим, якщо r_emp має додатне значення – зв’язок прямий.

У випадку, коли ׀r_emp׀ < r_krit, говорять, що лінійний зв’язок між двома досліджуваними параметрами відсутній.

Порядкова або рангова кореляція (за Спірменом)

Порядкову кореляцію можна застосовувати не тільки для порядкових, а й для інтервальних шкал.

Обчислюється коефіцієнт порядкової кореляції (ρ) за формулою:

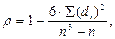{Формула 2.12}

де d_i = (х^/ - y^/) – різниця рангів об'єкта за ознаками, між якими встановлюється зв'язок

х^/ – ранг значення першої ознаки (х_і);

y^/ – ранг значення другої ознаки (y_і);

n – об’єм вибірки.

Ранги значень знаходять таким чином:

1) розташовують значення у висхідному (або низхідному) порядку;

2) кожному значенню приписується ранг. Ранг – це порядковий номер (місце) конкретного значення у впорядкованому ряді;

3) якщо два (або більше) учні отримали однакові значення, то рангом буде для цих значень середнє арифметичне їхніх порядкових номерів (місць) у ряду. Наприклад, проранжуємо таку сукупність оцінок учнів з навчального предмету: 7, 8, 8, 6, 5, 8, 8, 10. Розмістимо ці дані у табл.11.

Таблиця 2.15

Дата добавления: 2014-12-07