Расчеты по валам и их опорам

Определяющим критерием расчета валов главного привода является их жесткость в местах расположения зубчатых колес (при достаточной жесткости по прогибу и углу поворота прочность, как правило, обеспечивается с запасом). При курсовом проектировании рассчитываем суммарные прогибы и углы поворота двух соседних валов под соединяющими их зубчатыми передачами (в плоскости действия окружных сил) и сравниваем их с допустимыми.

Предварительно составляем расчетную схему одного из выбранных валов, которая позволит, помимо расчета жесткости, найти реакции в опорах для расчета подшипников.

7.2.1. Составление расчетной схемы и определение реакций в опорах.

Рассмотрим последовательность действий на примере расчета вала II (рис. 3.4.). Согласно кинематической схеме и конструктивной разработке строим схему действия на вал II сил в поперечном сечении (рис. 7.1.). При работе в наиболее нагруженном диапазоне 1 на вал действует окружная 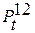и радиальная силы в зацеплении колес Z₁/Z₂, а также окружная и радиальная 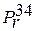силы в зацеплении колес Z₃/Z₄. Эти силы находятся в двух взаимно перпендикулярных плоскостях 1-1 и 2-2, одна из которых (пл. 1-1) всегда должна совпадать с линией действия окружной силы рассчитываемой далее передачи.

Примечание: Если центр вала III не находится на одной прямой, соединяющей центры валов 1 и 2 (и, следовательно, окружные силы P¹² _t и Р³⁴_t не параллельны), то рассматриваются проекции сил Р³⁴_t и P³⁴_r на плоскости 1-1 и 2-2. Углами отклонения до 20° можно в первом приближении пренебречь.

Расчетная схема вала II в плоскостях 1-1 и 2-2 приведена на рис.7.2. Окружные силы Р_t, согласно рис. 7.1., действует в одном направлении, а радиальные P_r – навстречу друг другу.

Величины действующих сил Р_t и P_r определены в п.6. Значения линейных размеров a, b, l в соответствии с разработанной конструкцией составляют
a = 50мм, b=80мм, l=300мм.

Реакции в опорах для расчета подшипников определяем по известным зависимостям (уравнениям моментов) из курса сопротивления материалов.

Для плоскости 1-1:

Проверка:

Для плоскости 2-2:

;

.

Проверка:

Суммарные реакции в радиальных опорах

;

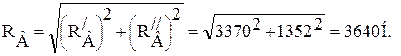
Расчет долговечности подшипников производится по стандартным общемашиностроительным методикам, изложенным в справочниках (например, [10]). Для опор шпинделя – см. раздел 9.

7.2.2. Расчет жесткости.

Необходимая жесткость валов при изгибе определяется условиями правильной работы зубчатых передач [14]. Для передач, расположенных вблизи середины пролета, проверяют жесткость по прогибу. Для передач, расположенных вблизи опор – жесткость по углу поворота. В промежуточных случаях производят обе проверки.

Прогибы и углы наклона упругой линии валов определяют обычными методами сопротивления материалов [например, [9]]. Для простых случаев следует пользоваться табл. 7.4. [14]. Прогибы и углы наклона определяются отдельно от всех сил на ведущем и ведомом валах, а затем алгебраически суммируются.

Допустимые величины суммарных прогибов под зубчатыми передачами D=(0,01…0,02)m, где m – модуль данной передачи.

Угол взаимного наклона валов под зубчатыми колесами должен быть меньше 0,001 радиан [14].

В качестве примера определим угол взаимного наклона валов I и II под передачей Z₁/Z₂. Расчетная схема для вала I приведена на рис.7.3, а для вала II – на рис.7.2., плоскость 1-1.

Для вала I l =300мм, a =50мм, Ø60мм.

Угол наклона вала I под силой P_t¹²=2000H по формулам табл. 7.4.

.

Здесь F= P_t¹²=2000H;

a_табл=а=50мм;

l _табл= l =300мм;

b_табл= l -a=300-50=250мм;

Е=2,1∙10⁵ Н/мм² – модуль упругости стали;

J=0,05×d⁴=0,05∙60⁴=65∙10⁴ мм⁴ – момент инерции сечения вала.

Таблица 7.4.

Угол наклона вала II Æ45 мм под силой P_t¹²=2000 Н по формулам табл. 7.4.

.

Здесь F= P_t¹²=2000H;

a_табл=а=50мм;

l _табл= l =300мм;

b_табл= l -a=300-50=250мм;

Е=2,1∙10⁵Н/мм²;

J=0,05d⁴=0,05∙45⁴=20,5∙10⁴мм⁴.

Угол наклона вала II под силой P_t¹² от действия силы P_t³⁴ по формулам табл. 7.4.

.

Здесь F= P_t³⁴=4140H;

b_табл=b=80мм;

l _табл= l =300мм;

d_табл=a=50мм;

Е=2,1∙10⁵Н/мм²;

J=20,5∙10⁴мм⁴.

Суммарный угол наклона вала II под передачей Z₁/Z₂

θ_II= θ_F2+ θ_d=(12,9+32,6)×10^-5=45,5∙10^-5рад

Угол взаимного наклона валов I и II

Θ_1-2=θ_F1+ θ_II=(4,07+45,5)×10^-5=49,6∙10^-5≈0,0005рад<0,001рад.

Жесткость валов под передачей Z₁/Z₂ удовлетворительна.

Дата добавления: 2014-12-07