Розв’язок. Відношення є функцією з в , тому що

Розв’язок.

Розв’язок.

Розв’язок.

Відношення 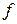є функцією з 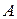в 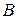, тому що 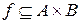, і кожний з елементів 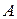присутній як перший компонент упорядкованої пари з 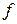рівно один раз.

Завдання 2. Нехай , 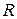- множина дійсних чисел. Знайти область визначення та область значень функції .

Область визначення функції 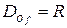(множина дійсних чисел), область значень функції .

Завдання 3. Знайти обернену функцію для .

Обертаючи функцію, одержуємо 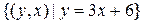. Це те ж саме, що 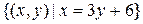. Вирішуючи рівняння відносно 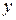, одержуємо .

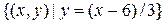Завдання 4. Нехай 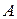в 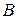- множина дійсних чисел, і функція 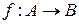визначена як . Чи є функція сюр’єкцією, ін’єкцією й бієкцією?

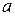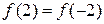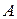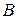Функція не є сюр’єктивною, оскільки не існує такого дійсного числа , для якого . Функція не є ін’єктивною, тому що , але . Помітимо, якщо і - множина додатних дійсних чисел, тоді функція 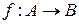є ін’єктивною і сюр’єктивною.

4 БУЛЕВІ ФУНКЦІЇ ТА ПЕРЕТВОРЕННЯ

4.1 Мета заняття

Ознайомлення на практичних прикладах з основними поняттями булевої алгебри. Вивчення способів задання булевих функцій. Аналіз формул і тотожностей, які визначають властивості операцій булевої алгебри. Вивчення і використання методів доведення тотожностей булевої алгебри.

4.2 Методичні вказівки з організації самостійної роботи студентів

Під час підготовки до практичного заняття необхідно повторити лекційний матеріал, розділи літератури [1-8] з наступних питань: булеві змінні і булеві функції (основні поняття); область визначення та область значень булевої функції; способи задання булевих функцій; побудова таблиць істинності булевих функцій; реалізація булевих функцій формулами; принцип двоїстості в булевій алгебрі; булеві алгебри, закони і тотожності булевої алгебри.

Підготовка і виконання практичного заняття проводиться за два етапи.

Перший етап пов’язаний з вивченням на практичних прикладах наступних основних понять і визначень булевої алгебри: булеві змінні; булеві функції; номери булевих функцій та інтерпретацій; інтерпретація булевої функції; n-мірний булевий куб; область визначення булевої функції; таблиця істинності (відповідності) булевої функції; заперечення, кон’юнкція, диз’юнкція, еквіваленція, імплікація, стрілка Пірса, штрих Шеффера; булева формула; суперпозиція булевих функцій; пріоритет операцій булевої алгебри; інфіксний запис формул; еквівалентні формули та перетворення булевих функцій; двоїста функція; самодвоїста функція; принцип двоїстості; двохелементна булева алгебра; алгебра логіки; еквівалентні (рівносильні) формули булевих функцій.

При виконанні першого етапу практичного заняття студент повинен запропонувати і записати індивідуальний приклад для кожного з розглянутих вище понять і визначень.

Другий етап виконання практичного заняття пов’язаний з розв’язанням практичних завдань, представлених у підрозділі 4.3, на основі запропонованих типових прикладів (див. підрозділ 4.4).

4.3 Контрольні запитання і завдання

4.3.1 Контрольні запитання

1. Які змінні називаються булевими або логічними змінними?

2. Яка функція називається логічною (булевою, перемикальною)?

3. Наведіть приклади завдання (використання) булевих змінних у мовах програмування.

4. Як називається сукупність конкретних значень аргументів булевої функції?

5. Скільки елементів-слів містить 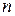-мірний булевий куб?

6. Що являє собою область визначення та область значень булевої функції?

7. Як визначити число всіх булевих функцій, що залежать від 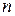змінних?

8. Перелічить способи задання булевих функцій.

9. Що являє собою таблиця істинності (відповідності) булевої функції. Назвіть правила її побудови.

10. Перелічить булеві функції від однієї змінної, від двох змінних.

11. Яким чином визначається номер булевої функції? Як визначається номер інтерпретації?

12. Дайте визначення формули для задання булевої функції. Що таке суперпозиція булевих функцій?

13. Які знаки використовуються при побудові формул? Який пріоритет визначений для операцій алгебри логіки?

14. Який запис формул називається інфіксним? Наведіть приклади.

15. Чим відрізняється табличний і формульний спосіб задання булевих функцій? У яких випадках застосовується кожний з них?

16. Які формули називаються рівносильними або еквівалентними?

17. Перелічить основні методи визначення рівносильності формул.

18. Надайте визначення двоїстої і самодвоїстої функції.

19. Яким чином формується таблиця істинності двоїстої функції?

20. Сформулюйте принцип двоїстості булевих функцій.

21. Надайте визначення двохелементної булевої алгебри та алгебри логіки.

22. Перелічить основні закони булевої алгебри.

23. Яким способом можна довести закони булевої алгебри.

24. Сформулюйте і запишіть тотожності для законів булевої алгебри.

4.3.2 Контрольні завдання

Завдання 1. У скільки разів більше різних двійкових слів треба аналізувати для булевої функції , чим для булевої функції ?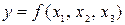

Завдання 2. У скільки разів більше можна побудувати булевих функцій, що залежать від 6-и змінних, чим від 4-х змінних?

Завдання 3. Побудувати таблиці істинності наступних функцій і визначити їхній порядковий номер:

а) ;

б) ;

в) ;

г) ;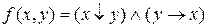

д) .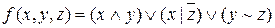

Завдання 4. Перевірити за допомогою таблиць істинності, чи справедливі наступні співвідношення:

а) ;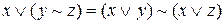

б) ;

в) ;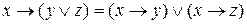

г) ;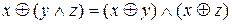

д) .

Завдання 5. При 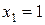; ; 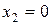; 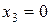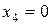знайдіть значення функцій 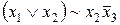і .

Завдання 6. Довести, що імплікація та еквіваленція може бути визначена через інші функції: ; .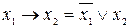

Завдання 7. Використовуючи основні еквівалентності, довести еквівалентність формул 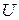і 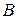, якщо , .

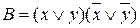Завдання 8. Знайти двоїсті формули до наступних функцій:

а) ;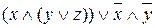

б) ;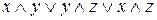

в) .

Завдання 9. Визначити, чи є наступні функції самодвоїстими:

а) ;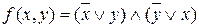

б) ;

в) .

Завдання 10. Спростити за допомогою законів булевої логіки наведені нижче вирази. Потім за допомогою таблиць істинності зрівняти отримані вирази із заданими:

а) ;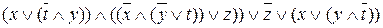

б) ;

в) .

Завдання 11. Булева функція 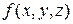визначається таким чином: вона дорівнює 1 при , або, якщо 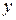і 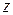приймають різні значення, а значення змінної 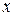менше значення змінної 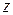. В інших випадках функція дорівнює 0. Скласти таблицю істинності функції 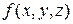і записати множину .

4.4 Приклади аудиторних і домашніх завдань

Завдання 1. Визначити потужність множини двійкових слів (інтерпретацій), на яких визначена булева функція .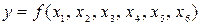

Дата добавления: 2014-12-07