
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
К) внутри тороида на произвольном расстоянии r от его центра
|
|
|
|
З) внутри соленоида конечной длины
B = mm0nI/2; H = nI/2; (5.25)
и) внутри тороида на его оси (тороид - соленоид, свитый в кольцо)
B = mm0IN/l = mm0In = mm0IN/2pr; H = IN/l = In = IN/2pr; (5.26)
B = mm0nIR/r; H = nIR/r, (5.27)
где l = 2pr - длина оси тороида;
R – радиус тороида по средней линии;
r - радиус тороидального кольца;
I - сила тока;
N - число витков тороида;
n - число витков на единицу длины тороида.
Циркуляция вектора индукции магнитного поля по замкнутому контуру L (или просто циркуляцией вектора индукции магнитного поля) – физическая величина, определяемая линейным интегралом:
 , (5.28)
, (5.28)
где d l – вектор элементарной длины замкнутого контура, направленной вдоль обхода контура;
Bl = B×cosa - составляющая вектора B в направлении касательной к контуру (с учетом выбранного направления обхода);
a - угол между векторами B и d l.
Циркуляция вектора напряженности магнитного поля по замкнутому контуру L (или просто циркуляция вектора напряженности магнитного поля) - физическая величина, определяемая линейным интегралом:
 , (5.29)
, (5.29)
где d l – вектор элементарной длины замкнутого контура, направленной вдоль обхода контура;
Hl = H×cosa - составляющая вектора H в направлении касательной к контуру (с учетом выбранного направления обхода);
a - угол между векторами H и d l.
Закон полного тока (теорема о циркуляции индукции магнитного поля) в интегральной форме: циркуляция вектора индукции магнитного поля по замкнутому контуру L равна произведению mm0 на алгебраическую сумму токов, охватываемых контуром (направление обхода контура и направление тока должны быть связаны между собой правилом правого винта):
 , (5.30)
, (5.30)
где n – число проводников с токами, охватываемых контуром L произвольной формы.
Следствия из закона полного тока:
1) если направление обхода контура и направление тока в проводнике не связаны между собой правилом правого винта, то значение циркуляции вектора магнитной индукции, сохранив величину, изменит знак;
2) если контур, расположенный в магнитном поле, не охватывает ток или алгебраическая сумма токов внутри замкнутого контура равна нулю:
 . (5.31)
. (5.31)
Закон полного тока (теорема о циркуляции индукции магнитного поля) в дифференциальной форме справедлив для произвольных токов и контуров:
rot B =mm0 j. 5.32
Условие непотенциальности магнитного поля (вихревого характера магнитного поля):
 . (5.33)
. (5.33)
Поток магнитной индукции (магнитный поток) через площадку dS - физическая величина, численно равная произведению проекции B на направление положительной нормали n и величины этой площадки dS:
dФm=Bn×dS=B×dS×cosa, (5.34)
где a - угол между векторами Bиn;
Bn = B×cosa - проекция вектора B на направление положительной нормали к площадке dS.
Полный поток магнитной индукции через некоторую поверхность S
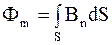 . (5.35)
. (5.35)
Для однородного магнитного поля и плоской площадки S
Фm = Bn×S. (5.36)
Теорема Остроградского-Гаусса для магнитных полей:
 . (5.37)
. (5.37)
Индукция магнитного поля B в магнитной цепи, состоящей из стального сердечника с воздушным (вакуумным) зазором:
 , (5.38)
, (5.38)
где lc, lВ - соответственно длина стального и воздушного участков цепи;
mс, mВ - их магнитные проницаемости;
I - ток в обмотке цепи;
N - число витков обмотки.
Закон Ома для магнитных цепей:
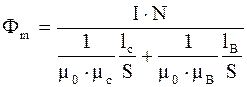
 , (5.38)
, (5.38)
где I×N = Eм - магнитодвижущая сила;
Rмс =  - магнитное сопротивление цепи сердечника;
- магнитное сопротивление цепи сердечника;
Rмв = 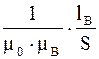 - магнитное сопротивление цепи воздушного зазора;
- магнитное сопротивление цепи воздушного зазора;
Rм = Rмс + Rмв - полное сопротивление магнитной цепи.
Законы (правила) Кирхгофа для магнитных цепей:
1. Первый: Алгебраическая сумма магнитных потоков в участках цепи, сходящихся в узле, равна нулю:
 . (5.39)
. (5.39)
Примечание: знак Фмi определяется направлением соответствующих линий B. Если линии вектора B сходятся в узле, Фмi - положителен, если они выходят из узла, Фмi - отрицателен.
2. Второй: В любом замкнутом магнитном контуре, произвольно выбранном в разветвленной магнитной цепи, алгебраическая сумма произведений магнитных потоков на магнитное сопротивление соответствующих участков цепи равна алгебраической сумме магнитодвижущих сил этого контура:
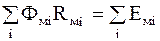 . (5.40)
. (5.40)
При последовательном соединении магнитопроводов полное магнитное сопротивление равно сумме магнитных сопротивлений отдельных последовательно соединенных участков:
Rм =  . (5.41)
. (5.41)
При параллельном соединении величина, обратная сопротивлению разветвленной части магнитной цепи, равна сумме обратных величин магнитных сопротивлений отдельных ветвей:
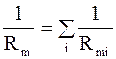 . (5.42)
. (5.42)
5.2. Силы, действующие на ток в электромагнитном поле
Сила, действующая в магнитном поле на элемент объема тела dV:
d F =e [ v ´ B ]∙dN = n∙e∙[ v ´ B ]dV = [ j ´ B ]dV, (5.43)
где e- величина заряда электрона;
n - концентрация свободных электронов;
dN = n∙dV - число заряженных частиц в объеме dV;
j= nev - плотность тока;
v - скорость направленного движения свободных электронов;
B - индукция магнитного поля.
Сила (сила Ампера), действующая на проводник с током в магнитном поле (закон Ампера):
а) на каждый элемент проводника dl
d F = I×[d l ´ B ]; (5.44)
б) на проводник конечной длины

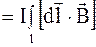 , (5.45)
, (5.45)
где l длина проводника.
Величина силы, действующей со стороны однородного магнитного поля на прямолинейный проводник с током:
F = I∙B∙l∙sina. (5.46)
Величина силы, действующей со стороны неоднородного поля и проводника произвольной формы:
dF = I∙B∙dl∙sina. (5.47)
5.3. Работа по перемещению проводника и контура с током в магнитном поле
Работа по перемещению проводника с током в магнитном поле (работа, совершаемая силами Ампера), ток в котором постоянен, равна произведению силы тока на величину магнитного потока через поверхность, которую описывает проводник при своем движении:
dA = I×dФm. (5.48)
Работа по перемещению проводника с током в магнитном поле (работа, совершаемая силами Ампера), ток в котором постоянен и проводник прямолинейный:
A = I×DФm. (5.49)
Работа, совершаемая силами Ампера при перемещении в магнитном поле контура, ток в котором постоянен, равна произведению силы тока на изменение магнитного потока через поверхность, ограниченную контуром:
dA = I×dФm, (5.50)
где I - величина тока в контуре;
dФm - изменение магнитного потока.
Работа, совершаемая силами Ампера при перемещении в магнитном поле контура, ток в котором постоянен, а перемещаемый контур состоит из N витков:
dA = 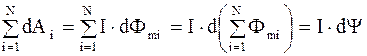 , (5.51)
, (5.51)
где Y =  - потокосцепление или полный магнитный поток, пронизывающий N витков контура.
- потокосцепление или полный магнитный поток, пронизывающий N витков контура.
5.4. Магнитные свойства вещества (среды)
Диамагнетики - вещества (среда), намагничивающиеся во внешнем магнитном поле напряженностью H в направлении, противоположном направлению вектора H (приобретающие суммарный магнитный момент, который направлен противоположно вектору H).
Диамагнетизм (диамагнитный эффект) – свойства вещества намагничиваться навстречу направлению действующего на него внешнего магнитного поля. При этом вектор намагничивания J пропорционален напряженности внешнего магнитного поля H:
J =  æ
æ 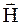 = æ
= æ  , (5.52)
, (5.52)
где æ=  - диамагнитная восприимчивость вещества.
- диамагнитная восприимчивость вещества.
Примечания:
1) диамагнетизм - свойство, присущее любым веществам, так как он обусловлен действием внешнего магнитного поля на электронные орбиты атомов и молекул;
2) движение электронов по орбитам сопровождается появлением магнитного поля, направленного против внешнего поля и ослабляющего его (закон Ленца);
3) диамагнитный эффект не связан с появлением упорядоченности в расположении электронных орбит, поэтому диамагнитная восприимчивость æ не зависит от температуры;
4) диамагнитный эффект является реакцией вещества на воздействие внешнего магнитного поля.
Магнитный момент электрона, представляющего собой некоторый эквивалентный круговой ток:
pm = I∙S = e∙n×pr2 = e×vo×r/2, (5.53)
где e - заряд электрона;
vo - его скорость;
r - радиус орбиты;
n – частота, с которой электрон движется по орбите.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 556; Нарушение авторских прав?; Мы поможем в написании вашей работы!