Ядерный магнетон

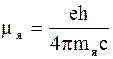. (5.64)

Спиновый магнитный момент

m_S = 2m_Б 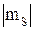. (5.65)

Парамагнитная восприимчивость диэлектриков согласно классической теории Ланжевена определяется формулой

æ_L = 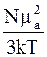, (5.66)

где N - число парамагнитных атомов в 1 моле вещества;

m_а - магнитный момент атома.

Магнитная восприимчивость диэлектриков с точки зрения квантовой теории парамагнетизма учитывает пространственное квантование момента m_а и при m_аH<<kT приводит к следующей формуле:

æ_L = 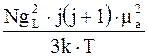, (5.67)

где j - квантовое число, определяющее полный момент импульса атома;

g_L - множитель Ланде.

Парамагнитная восприимчивость одного моля:

а) для полупроводников æ_п обусловлена электронами проводимости, в простейшем случае зависит от температуры T экспоненциально:

æ 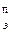= AT^1/2×exp(-DE/kT), (5.68)

где A - константа вещества;

DE - ширина запрещенной зоны полупроводника;

б) для металлов - без учета диамагнетизма Ландау и взаимодействия электронов

æ 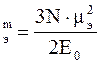, (5.69)

где E_o - энергия Ферми;

m_э - магнитный момент электрона.

Ядерный парамагнетизм при отсутствии сильного взаимодействия между спинами ядер и электронными оболочками атомов возникает, в основном, за счет двух факторов:

1) орбитального движения электронов (полный орбитальный магнитный момент атома является суммой орбитальных магнитных моментов отдельных электронов);

2) наличия у каждого электрона собственного магнитного момента, связанного со спином электрона, т.е. собственного механического момента электрона; характеризуется величиной

æ_я = 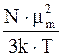. (5.70)

Ферромагнетик – вещество (среда), в котором ниже определенной температуры (точки Кюри) устанавливается ферромагнитный порядок магнитных моментов атомов или ионов (в неметаллических кристаллах) или магнитных моментов коллективизированных электронов (в металлических кристаллах).

Ферромагнетизм - магнитоупорядоченное состояние вещества, при котором все магнитные моменты атомов в веществе параллельны.

Магнитная восприимчивость æ_k ферромагнетиков положительна и æ_k>>0.

Точка Кюри – температура, при которой намагниченность насыщения J_s равна нулю.

Обменное взаимодействие – взаимодействие, приводящее к ферромагнетизму, которое характеризуется напряженностью эффективного молекулярного поля:

H_эфф = A∙J_s. (5.71)

Энергия обменного взаимодействия U квадратично зависит от J_s:

U = -H_эффJ_s = 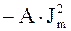, (5.72)

где A - постоянная молекулярного поля (A>0);

J_s - намагниченность насыщения.

Закон Блоха: с точки зрения теории спиновых волн, при низких температурах самопроизвольная намагниченность убывает с ростом температуры

J_s = J_so(1 - aT^3/2), (5.73)

где J_so - намагниченность насыщения при T = 0.

Домены – области однородной намагниченности в ферромагнетике в отсутствие внешнего магнитного поля.

Коэрцитивная сила H_c – величина напряженности магнитного поля, в котором ферромагнетик, первоначально намагниченный до насыщения, размагничивается.

Остаточная индукция B_s – величина, характеризующая магнитное поле в ферромагнетике даже в отсутствие внешнего магнитного поля.

Остаточная намагниченность J_r – намагниченность J_r, которую имеет ферромагнетик при напряженности внешнего магнитного поля H = 0.

Намагничивание – процессы установления намагниченности, протекающие в веществе при действии на него внешнего магнитного поля:

а) в диамагнетиках намагничивание состоит в возникновении микроскопических индукционных токов, создающих намагниченность, направленную против внешнего магнитного поля;

б) в парамагнетиках намагничивание состоит из ориентации хаотически колеблющихся магнитных моментов атомов или ионов в направлении внешнего магнитного поля;

в) в ферромагнетиках намагничивание состоит в переориентации векторов намагниченности доменов в направлении внешнего магнитного поля. Включает процессы смещения, вращения и парапроцесс.

Процесс смещения в многодоменном ферромагнетике заключается в перемещении границ между доменами.

Процесс вращения состоит в повороте векторов J _s в направлении вектора H внешнего магнитного поля.

Парапроцесс (истинное намагничивание) – возрастание абсолютной величины самопроизвольной намагниченности J _s ферро - и ферримагнетиков под действием внешнего магнитного поля H. Обусловлен ориентацией в поле H элементарных носителей магнетизма (спиновых и орбитальных магнитных моментов атомов или ионов), оставшихся не повернутыми в направлении результирующей намагниченности вследствие «дезорганизующего» действия теплового движения.

Кривые намагничивания – графики, таблицы и формулы, показывающие зависимость намагниченности J или магнитной индукции B от напряженности внешнего магнитного поля H.

Ферримагнетик - вещества, в которых при температурах ниже точки Кюри T_c существует ферримагнитное упорядочение магнитных ионов.

Ферримагнетизм - магнитоупорядоченное состояние вещества, в котором магнитные моменты атомных носителей магнетизма образуют несколько магнитных подрешеток с магнитными моментами, направленными навстречу друг к другу или имеющими более сложную пространственную ориентацию; отличная от нуля векторная сумма намагниченностей подрешеток определяет самопроизвольную намагниченность вещества J_s.

Антиферромагнетизм - магнитоупорядоченное состояние вещества, характеризующееся тем, что магнитные моменты соседних частиц вещества - атомных носителей магнетизма - ориентированы навстречу друг другу (антипараллельно), и поэтому намагниченность тела в целом в отсутствие магнитного поля равна нулю.

Магнитострикция - изменение формы и размеров ферромагнетиков и ферримагнетиков при их намагничивании.

Магнитоупругий эффект (эффект Виллари) - обратное по отношению к магнитострикции явление - изменение намагниченности ферромагнитного образца при деформации.

Магнитное охлаждение - метод получения температур ниже 1К путем адиабатического размагничивания парамагнитных веществ.

Магнетокалорический эффект - изменение температуры магнетика при адиабатическом изменении напряженности магнитного поля H, в котором он находится.

На границе раздела двух магнетиков (сред):

а) нормальные составляющие вектора B и тангенциальные составляющие вектора H непрерывны:

B_1n = B_2n, H_2t = H_1t; (5.74)

б) закон преломления силовых линий векторов B и H при переходе через границу раздела двух магнетиков имеет вид

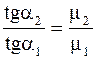. (5.75)

5.5. Основные уравнения термодинамики магнетиков

Первое начало термодинамики для магнетика:

dQ = dU + dA, (5.76)

где dQ - количество сообщенного тепла;

dU - изменение внутренней энергии;

dA - работа магнетика, которая складывается из работы dA' = pdV против внешнего давления и работы магнитного поля .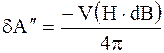

Основные уравнения термодинамики магнетиков для:

а) свободной энергии

F = U - TS, dF = -SdT + (H dB)/4p; (5.77)

б) термодинамического потенциала

Ф = F - H×B/4p; dФ = -SdT - (B dH)/4p; (5.78)

в) энтальпии

I = U - H.B/4p, dI = TdS - (B dH)/4p; (5.79)

г) изменения внутренней энергии

dU = TdS + (H dB)/4p; (5.80)

д) внутренней энергии магнетика U

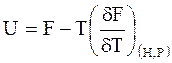. (5.81)

Дата добавления: 2014-12-07