Приближенная количественная теория атома гелия

Задача о движении двух электронов в поле ядра аналогична задаче о движении двух планет в гравитационном поле Солнца. В небесной механике разработаны достаточно точные приближенные методы расчета движения планет. В их основе лежит теория возмущений, использующая тот факт, что взаимодействие между планетами мало по сравнению с взаимодействием каждой планеты с Солнцем.

В нулевом приближении взаимодействием между планетами можно совсем пренебречь. Используя решение, полученное в нулевом приближении, можно затем учесть взаимодействие между планетами в первом приближении, после этого найти второе приближение и т.д.

Таким же методом решается задача и в квантовой механике. В нулевом приближении не учитывается взаимодействие электронов друг с другом. Но в квантовой механике энергия взаимодействия электронов друг с другом все-таки не мала, а сравнима с энергией взаимодействия каждого электрона ядром. Однако получающиеся результаты довольно удовлетворительны, чем и оправдывается использование методов теории возмущений.

Итак, для решения уравнения Шредингера

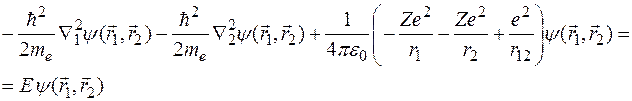
в нулевом приближении энергию взаимодействия электронов друг с другом

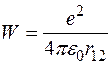
учитывать не будем.

Оставшийся Гамильтониан представим в виде

,

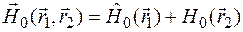где

, .

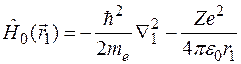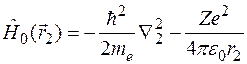Каждый из этих операторов имеет собственные функции 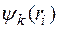и собственные значения .

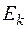Таким образом, в нулевом приближении уравнении Шредингера принимает вид

.

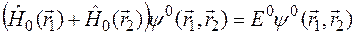Его собственными значениями будет сумма собственных значений энергии электронов в кулоновском поле ядра

,

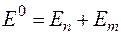а собственными функциями будут функции, равные произведению волновых функций электронов в одноэлектронных ионах

, .

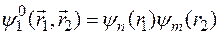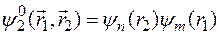Сами по себе эти функции не являются ни симметричными ни асимметричными, но из них можно построить линейную комбинацию

.

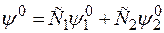При 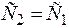получается симметричная координатная функция

,

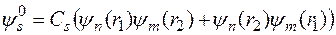при 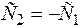- антисимметричная

.

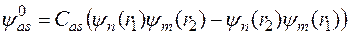Нормировочные постоянные равны .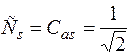

Отметим, что в нулевом приближении собственные значения энергии пара- и ортогелия совпадают.

Представим теперь энергию возмущения 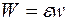, где 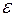- некоторый малый параметр. Тогда волновую функцию и энергию произвольного состояния можно представить в виде разложения по малому параметру

,

.

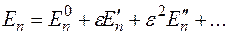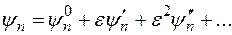Подставим эти разложения в исходное уравнение Шредингера

.

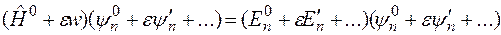Оставляя в этом уравнении слагаемые первого порядка малости получим

.

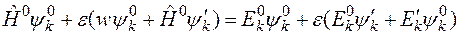Так как 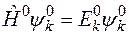, то получаем уравнение

.

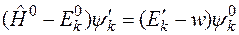Это неоднородное уравнение для определения 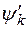с неопределенным параметром .

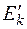Чтобы это уравнение имело непрерывные решения необходимо, чтобы его правая часть была ортогональна к решению однородного уравнения

,

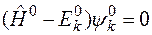т.е. к . Это значит, что

.

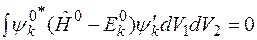Умножим неоднородное уравнение на 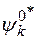и проинтегрируем по всем переменным

.

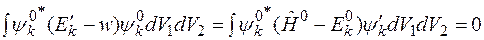Отсюда следует

.

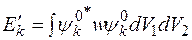Следовательно, поправка первого порядка к энергии невозмущенного состояния в атоме гелия вычисляется по формуле

.

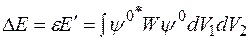Подставляя сюда волновые функции нулевого порядка, получим

,

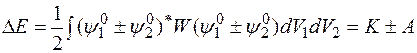где введены обозначения

,

.

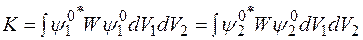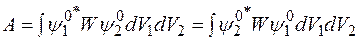Верхний знак относится к симметричным координатным функциям (антипараллельной ориентации спинов), нижний знак относится к антисимметричным координатным функциям (параллельной ориентации спинов).

Таким образом, для парагелия энергия состояний вычисляется по формуле

,

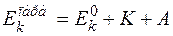для ортогелия

.

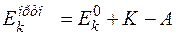Дата добавления: 2014-11-29