Энергетические уровни и спектральные серии щелочных металлов

В атомах щелочных металлов электронная оболочка содержит один наружный (валентный) электрон, сравнительно слабо связанный с ядром атома. Переходы между энергетическими уровнями валентного электрона сопровождаются излучением или поглощением фотонов относительно низких (оптических) частот. Остальные 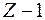электронов вместе с ядром образуют прочный остов, в электрическом поле которого движется валентный электрон.

При отсутствии валентного электрона распределение электрических зарядов в остове и его электрическое поле являются сферически симметричными. Наличие же валентного электрона эту симметрию нарушает из-за взаимного отталкивания электронов. Возникшая деформация в распределении электронов остова может быть описана суперпозицией мультиполей. Наибольший вклад в электрическое поле остова, кроме монополя, дает электрический дипольный момент, направленный к валентному электрону. Движение электронов в атоме является самосогласованным, т.е валентный электрон управляется электрическим полем внутренних электронов остова, но и они подвержены влиянию валентного электрона. В результате дипольный момент электронного остова всегда оказывается направленным к валентному электрону. Поэтому движение валентного электрона происходит так, как если бы поле остова оставалось центральным. В первом приближении соответствующая потенциальная функция может быть представлена в виде

.

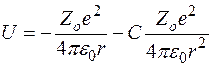Здесь второе слагаемое представляет энергию взаимодействие валентного электрона с диполем.

Уравнение для радиальной волновой функции в такой модели принимает вид

.

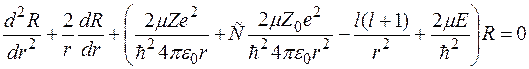Если ввести число 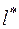, так, что

,

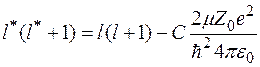то уравнение совпадет с уравнением для радиальной волновой функции в кулоновском поле.

Воспользовавшись собственными значениями этого уравнения, найдем

.

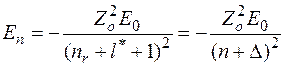Здесь 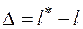, 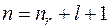- главное квантовое число.

Для 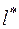получается выражение

.

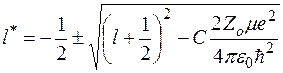Постоянная С с увеличением энергии состояния уменьшается и вторым слагаемым по корнем можно пренебречь. Для таких состояний 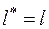. Поэтому перед корнем нужно брать верхний знак. Поэтому и для других состояний нужно так же брать верхний знак.

Величина поправки 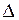зависит от главного квантового числа и от орбитального числа l.

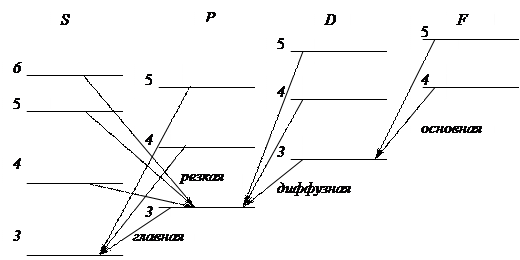Таким образом, в атомах щелочных металлов валентный электрон находится в поле остова. Заряд его нельзя считать точечным, поэтому электрическое поле нельзя считать обратно пропорциональным квадрату расстояния. Благодаря этому получается зависимость энергии валентного электрона не только от главного квантового числа, но и от орбитального. В этих условиях вырождение энергетических уровней по l снимается.

Квантовая механика смогла определить вероятности перехода из одного квантового состояния в другое. Оказалось, что вероятность дипольного излучения отлична от нуля, если орбитальное число изменяется на единицу 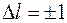. На изменение главного квантового числа никаких ограничений не накладывается.

В соответствии с правилами отбора в спектрах щелочных металлов получаются следующие серии:

Главная серия

;

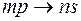Первая побочная, или диффузная, серия

;

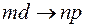Вторая побочная, или резкая, серия

;

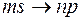Серия Бергмана, или фундаментальная, серия

.

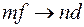На рисунке представлена схема уровней для и соответствующие разрешенные переходы.

Дата добавления: 2014-11-29