Атома водорода

Спин электрона. Тонкая структура спектра излучения

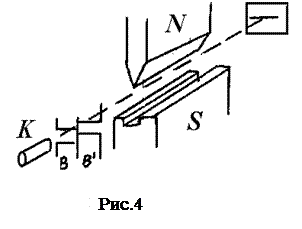
В 1921 году Штерном и Герлахом был поставлен прямой опыт по обнаружению квантования магнитного момента атомов. В вакуумной камере устанавливался электромагнит со специальной формой наконечников, чтобы создавать сильно неоднородное магнитное поле. Атомный пучок, формируемый испарителем К и системой щелей В,В', проходит вдоль полюсов магнита и попадает на экран (рис. 4).

В отсутствие магнитного поля на экране получалось четкое изображение щели. При включении сильно неоднородного магнитного поля на атомы действует сила, среднее значение которой определяется проекцией магнитного момента 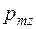и производной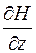

Если величина 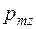принимает любые значения (непрерывна), то при прохождении через магнитное поле полоска Р на экране должна расплываться. Если 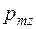принимает квантованные значения

,

то возможны (2l+1) различных проекций магнитного момента и на экране вместо одной полоски должны получаться (2l+1) полоски.

Опыт показал, что действительно из одной полоски получается несколько, т.е. квантование проекции магнитного момента было обнаружено, но число полосок было всегда четным, хотя величина (2l+1) всегда нечетная.

Кроме этого факта, не укладывающегося в теорию, было обнаружено спектральными методами, что энергетические уровни имеют тонкую структуру, т.е. состояние с энергией Е_n расщепляется на на два подуровня.

Для объяснения тонкой структуры спектров и опыта Штерна-Герлаха в 1925 году Дж.Уленбек и С. Гаудсмит выдвинули предположение, что помимо трех степеней свободы, определяемых тремя квантовыми числами n, l, m, существует четвертая - внутренняя степень свободы, и состояние электрона должно характеризоваться еще и четвертым квантовым числом. Согласно этой гипотезе у электрона есть собственный момент импульса, так называемый спин 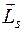, и связанный с ним собственный магнитный момент .

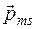Анализ опыта Штерна-Герлаха и дублетной структуры атома водорода привел к выводам, что

,

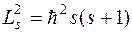где 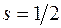– спиновое квантовое число.

Проекция спина на ось квантуется по обычным правилам

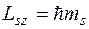
где – магнитное спиновое квантовое число, которое для электрона может принимать только два значения.

Первоначально считалось, что спин возникает из-за вращения электрона вокруг своей оси, но из опыта Штерна-Герлаха следует, что гиромагнитное отношение для спиновых моментов в два раза больше по величине, чем для орбитального движения, и для такого классического вращения заряженной частицы вокруг своей оси

В 1928 году Дирак показал, что спин электрона автоматически получается в релятивистской квантовой теории, и при этом получается правильное гиромагнитное отношение. В теории Дирака о внутренней структуре электрона никаких предположений не делалось.

Таким образом, спин электрона оказался квантово-релятивистским эффектом, не имеющим классического истолкования.

Паули показал как можно включить спин электрона в нерелятивистскую квантовую теорию, основанную на уравнении Шредингера. При этом необходимо учитывать взаимодействие орбитального и спинового магнитных моментов, что приводит к дополнительной энергии спин-орбитального взаимодействия, зависящей от взаимной ориентации угловых моментов.

Полный момент импульса 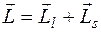, причем

,

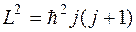где j – квантовое число полного углового момента. Оно принимает значения

.

Проекция полного момента определяется квантовым числом

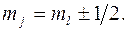
При заданном j возможны 2 j +1 квантовое состояние

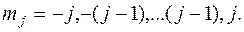
Число таких состояний у атомов с одним валентным электроном всегда четное, что и объясняет четность расщепления в опыте Штерна-Герлаха.

Наличие спин-орбитального взаимодействия приводит к тому, что энергия электрона зависит от квантового числа j

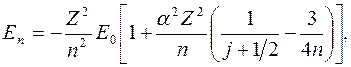
где 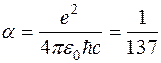– постоянная тонкой структуры.

Из-за малости величины 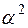поправка к нерелятивистской формуле получается очень малой. Энергия уровней зависит от n и j, но не зависит от l. Поэтому состояния с одним и тем же j, но разными l (разной ориентацией спинов) имеют одинаковую энергию.

В спектроскопии состояние электрона принято обозначать числами n, l, j, 2s+1 и заменять число l =0, 1, 2, 3, 4,... буквой s, p, d, f, g,..., соответственно.

Например, запись 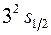означает, что электрон находится в состоянии с квантовыми числами n =3, l =0, j = , 2 s +1=2 (последняя цифра означает, что для атома с одним валентным электроном состояние является дублетом).

В состоянии 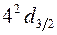квантовые числа имеют значения n = 4, l =2, j = 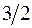, причем спин ориентирован вниз (). В состоянии – n =4, l =2, и спин ориентирован вверх ().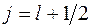

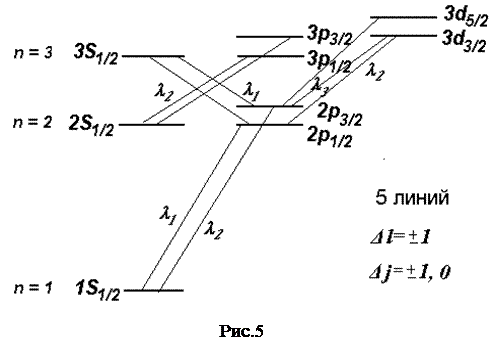
На рис.5 показана тонкая структура нижних уровней атома водорода и переходы между ними, в соответствии с правилами отбора ,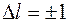

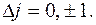
Тонкая структура энергетических уровней обуславливает тонкую структуру спектральных линий, так для перехода из состояния с n =2 в состояние с n =1 получаются две спектральные линии, а для перехода из состояния с n =3 в состояние с n =2 – пять спектральных линий.

Дата добавления: 2014-11-29