Спектр энергий в кулоновском поле

Используя выражение для оператора кинетической энергии радиального движения

,

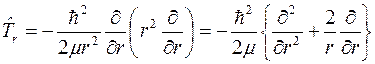уравнение (2) для электрона движущегося в кулоновском поле ядра

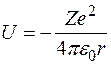
запишется в виде

.

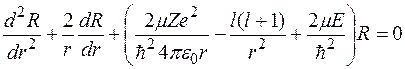Здесь 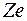- заряд ядра.

Сформулируем основные результаты, вытекающие из решения этого уравнения для атома водорода.

1. Спектр собственных значений энергии данного уравнения получается точно таким же, как в полуклассической теории Бора, причем квантовое число n = 1, 2,..., получается автоматически без введения дополнительных постулатов и называется главным квантовым числом. Главное квантовое число определяет величину энергии

,

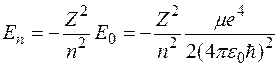где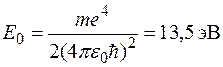

2. Собственные функции помимо главного квантового числа n определяются еще двумя квантовыми числами: орбитальным квантовым числом l и магнитным квантовым числом m и выражаются в виде произведения радиальной волновой функции 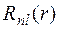и шаровой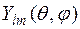

.

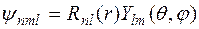3. Орбитальное квантовое число l определяет собственные значения квадрата углового момента (момента импульса)

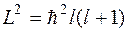
и принимает для заданного n целочисленные значения 0, 1, 2,..., n -1.

В состоянии с данной энергией Е_n квадрат момента импульса принимает n различных значений.

4. Магнитное квантовое число m определяет величину проекции момента импульса на выделенное направление

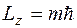
и для данного значения орбитального квантового числа принимает (2 l +1) значение 0, ±1, ±2,... ± l.

5. В классической физике с орбитальным движением электрона связан магнитный момент

,

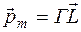где гиромагнитное отношение для электрона

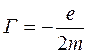
В квантовой физике это соотношение сохраняется для операторов и из него следует, что проекция магнитного момента на ось Z принимает 2 l +1 значение

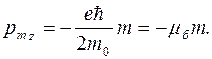
Здесь введено обозначение

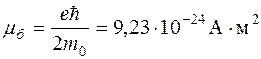
для кванта магнитного момента электрона, называемого магнетоном Бора.

6. Таким образом, три квантовых числа n, l, m и соответствующие им значения энергии Е_n , квадрата момента импульса 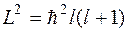и проекции момента импульса 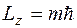полностью определяют волновую функцию электрона в атоме водорода 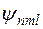. Число этих параметров равно числу степеней свободы. При этом получается, что состоянию с одной и той же энергией Е_n соответствует 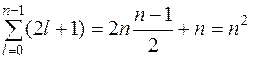различных состояний, отличающихся друг от друга значениями квадрата углового момента L² и проекции углового момента L_z на ось Z.

Различные квантовые состояния, соответствующие одной и той же энергии называются вырожденными. Решение уравнения Шредингера для атома водорода показало, что фактор вырождения (число состояний с одинаковой энергией) равен n².

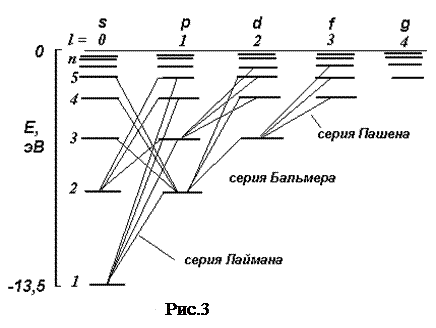
Состояния с заданным моментом импульса обозначаются малыми буквами латинского алфавита:

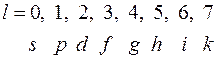
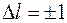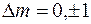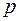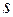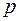Квантовая механика позволила не только вычислить спектр энергий в атоме водорода, но и сформулировала правила отбора для возможных переходов из одного состояния в другое. Разрешены переходы, для которых изменение орбитального квантового числа равно единице , а изменение магнитного квантового числа . Это значит, что разрешены переходы между состояниями и 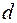, 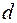и , и 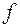и т.п., но не разрешены переходы между 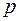и 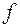состояниями.

Дата добавления: 2014-11-29