В системе однотипных микрочастиц реализуются только такие состояния, которые не меняются при перестановке местами двух любых микрочастиц

Принцип Паули

Принцип тождественности состояний неразличимых частиц.

1. Сочетание волновых и корпускулярных свойств у микрочастиц приводит к отличиям в поведении не только одиночных микрочастиц, но и в поведении коллективов частиц. Эти отличия касаются только систем однотипных частиц (электронов, протонов, атомов одного изотопа и т.д.), имеющих одинаковые массу, электрический заряд, спин и пр., т.е. физически неразличимых частиц.

Чтобы уяснить эти отличия будем рассматривать коллектив из двух микрочастиц (например, электронов). Отметим положения этих микрочастиц в некоторый момент времени, припишем им номера 1 и 2.

С классической точки зрения за дальнейшим движением таких частиц можно проследить (они двигаются по своим траекториям), т.е. всегда получить ответ на вопрос: какая из частиц имеет номер 1, а какая номер 2. Поменяв местами и скоростями обе частицы, мы получим состояние с теми же свойствами, что и предыдущее, но отличающееся от него нумерацией частиц.

Таким образом, по классическим законам одинаковые частицы индивидуализированы, т.е. принципиально различимы. Если поменять состояния у двух частиц (координаты и импульс одной частицы заменить координатами и импульсом другой частицы), то в классической физике получается новое состояние системы частиц.

Совсем иначе обстоит дело для микрочастиц, подчиняющихся квантовым закономерностям. Движение микрочастиц бестраекторно в силу принципа неопределенности, и проследить за движением микрочастиц объективно невозможно. Через некоторый промежуток времени мы не сможем сказать, какая из микрочастиц имеет номер 1, а какая – номер 2. Поэтому, если две микрочастицы поменять местами, то такого обмена физически обнаружить невозможно (одинаковые микрочастицы обезличены). Такой обмен не приводит к новому состоянию.

Эта особенность в поведении одинаковых микрочастиц формулируется в виде принципа неразличимости тождественных (однотипных микрочастиц).

2. Состояние системы микрочастиц описывается волновой функцией, зависящей от координат и спинов всех частиц. По-прежнему ограничимся рассмотрением системы из двух микрочастиц. Обозначим набор координат и проекции спина первой частицы символом 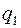, а второй - 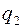; тогда волновая функция двух микрочастиц записывается в виде 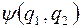. Здесь мы отвлекаемся от временной зависимости волновых функций. При перестановке частиц 1 и 2 мы получаем волновую функцию, которая должна описывать то же самое состояние. Это означает, что распределение вероятностей по набору переменных 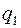и 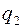, определяемое квадратом модуля волновой функции, будет одинаково в обеих ситуациях

.

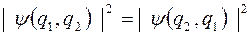При этом оказывается, что возможны два типа волновых функций, описывающих состояние системы: симметричные, у которых волновая функция не изменяется при перестановке частиц

,

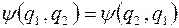и антисимметричные, у которых волновая функция изменяет знак при перестановке частиц

.

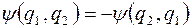Эти результаты справедливы для систем с любым числом частиц. Частицы, которые описываются симметричными волновыми функциями, называются бозонами, а которые описываются антисимметричными волновыми функциями – фермионами. Показано, что у бозонов спиновое квантовое число является целым или нулем, а у фермионов – полуцелым. К бозонам относятся фотоны, 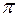- и К -мезоны. К фермионам относятся электроны, протоны, нейтроны, их античастицы и др. Кроме того, установлено, во-первых, что характер симметрии волновых функций с течением времени не изменяется, а во-вторых, бозоны и фермионы имеют разные статистики, т.е. различное распределение частиц по состояниям.

3. Сложные частицы, такие как атомы и ядра, также подразделяются на бозоны и фермионы в зависимости от суммарного спина частиц, составляющих атом или ядро. Так атом водорода состоит из протона и электрона, у которых спин равен . Суммарный спин атома водорода либо равен нулю (когда спины протона и электрона противоположны), либо единице (когда спины протона и электрона складываются). В обоих случаях атом водорода в нормальном состоянии будет бозоном.

Ядро атома гелия 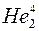состоит из четырех нуклонов со спином , поэтому спин этого ядра равен нулю и оно является бозоном.

Ядро атома гелия 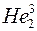состоит из трех нуклонов и спин его полуцелый, поэтому оно относится к фермионам. Ядра 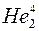подчиняются статистике Бозе-Эйнштейна, ядра 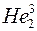- статистике Ферми-Дирака. Это проявляется в том, что вблизи абсолютного нуля температуры 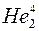обладает сверхтекучестью, а 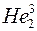не обладает.

4. Если частицы в системе не взаимодействуют, то волновая функция системы 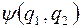может быть записана через волновые функции отдельных частиц. Обозначим волновую функцию первой частицы, находящейся в некотором состоянии 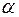- 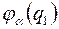, а волновую функцию второй частицы, находящейся в состоянии - .

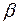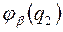Эти волновые функции являются решениями уравнений Шредингера для соответствующих частиц

,

,

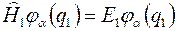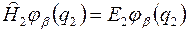где

,

,

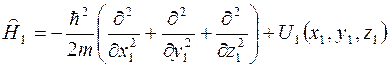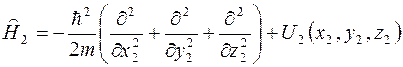- гамильтонианы первой и второй частицы (они действуют на координаты только своей частицы).

Гамильтониан системы невзаимодействующих частиц равен только сумме гамильтонианов отдельных частиц, поскольку нет оператора энергии взаимодействия частиц

.

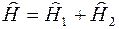Поэтому уравнение Шредингера для системы частиц

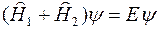(3)

можно решить, если положить

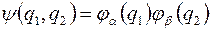, (4)

.

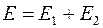Действительно подстановка (4) в (3) приводит к тождеству

.

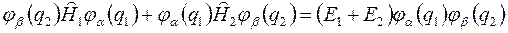Таким образом, для невзаимодействующих частиц волновая функция системы представляется в виде произведений волновых функций отдельных частиц. Но решение (4) само по себе не является ни симметричным, ни антисимметричным.

5. Поскольку, функция 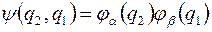в силу тождественности частиц также является решением уравнения Шредингера (она получается из (4), если поменять местами частицы 1 и 2), то из этих двух волновых функций можно составить линейные комбинации, которые также будут решениями уравнения (3)

,

,

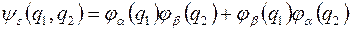но будут либо симметричны, либо антисимметричны относительно перестановки частиц.

Для невзаимодействующих частиц можно говорить, что система находится в таком состоянии, когда одна частица находится в состоянии 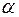, а другая в состоянии 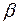. При этом волновые функции для фермионов и бозонов существенно различаются.

В системе одинаковых фермионов не может быть двух частиц, находящихся в одинаковых состояниях. Действительно, при 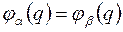антисимметричная волновая функция обращается в нуль, что означает, что вероятность нахождения системы в таком состоянии равна нулю. Таким образом, из симметрии волновой функции для системы невзаимодействующих фермионов следует, что в одном и том же состоянии два фермиона в системе находиться не могут. Это положение называется принципом Паули.

Хотя принцип Паули сформулирован для невзаимодействующих фермионов, тем не менее, он оказался плодотворным в объяснении периодического закона Д.И. Менделеева, а также некоторых закономерностей в спектрах атомов.

Поскольку состояние отдельного электрона определяется четверкой квантовых чисел, то Паули утверждал, что в атоме не может быть двух электронов, характеризующихся одинаковыми четверками квантовых чисел.

Для бозонов принцип симметрии волновых функций не накладывает ни каких ограничений, аналогичных запрету Паули.

Дата добавления: 2014-11-29