Спин-орбитальное взаимодействие

Основное взаимодействие электрона с ядром атома есть электростатическое взаимодействие их зарядов. Но так как электрон движется вокруг ядра, то возникает дополнительное взаимодействие, обусловленное относительным движением заряженных частиц: ядра и электрона. В существовании спин-орбитального взаимодействия можно убедиться наглядно, воспользовавшись представлениями полуклассической теории Бора, считая, что электрон движется вокруг ядра по круговой орбите радиуса r со скоростью .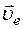

Если перейти в систему отсчета, связанную с электроном, то в такой системе движется ядро со скоростью . Движущееся в такой системе ядро создает магнитное поле

,

где

- вектор электрического смещения электрического поля, создаваемого ядром.

Дополнительная энергия электрона в таком магнитном поле, обусловленная ориентацией спинового магнитного момента равна

.

Величина потенциальной энергии взаимодействия электрона с ядром связана с энергией стационарного состояния соотношением

.

В стационарных состояниях радиус боровской орбиты выражается через радиус первой орбиты в атоме водорода

.

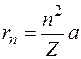С учетом этих формул для энергии спин-орбитального взаимодействия получаем выражение

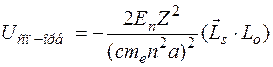
Энергия спин-орбитального взаимодействия по отношению к энергии кулоновского взаимодействия электрона с ядром является релятивистской поправкой порядка 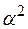, где - постоянная тонкой структуры.

Действительно, например, для основного состояния электрона в атоме водорода

,

так как .

Поэтому теория спин-орбитального взаимодействия должна быть релятивистской. Этого и следовало ожидать, так как сам спин есть квантово-релятивистский эффект, исчезающий в нерелятивистском приближении. В полуклассической теории к расщеплению энергетических уровней приводит так же зависимость массы от скорости.

Все релятивистские поправки зависят от 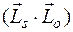, так что в целом оператор спин-орбитального взаимодействия, учитывающий все эффекты порядка пропорционален

.

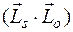
Собственные значения этого оператора выражаются через собственные значения оператора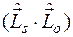

.

Так как , то при параллельной ориентации угловых моментов () энергия

оказывается больше, чем при антипараллельной ориентации

.

Наиболее последовательно тонкая структура спектра может быть рассчитана на основе релятивистской квантовой теории Дирака, в которой автоматически учитывается и спин электрона и зависимость массы от скорости.

Таким образом, каждый уровень энергии в атоме водорода и в водородоподобных ионах расщепляется на два, и энергия состояния зависит от 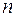и , но не зависит от орбитального числа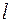

.

Иначе говоря в водороде и в водородоподобных ионах уровни энергии с одинаковыми квантовыми числами n и j, но различными l совпадают. Для остальных одноэлектронных атомов, например для атомов щелочных металлов, совпадения нет.

Дата добавления: 2014-11-29