Собственные значения оператора углового момента

Собственные значения 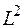и собственные функции 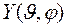оператора квадрата момента импульса находятся путем решения соответствующего операторного уравнения

.

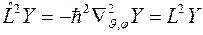Но собственные значения 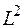можно определить с помощью одних только правил коммутации. Приведем эти правила к более удобному для этой цели виду, введя два оператора

, .

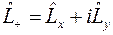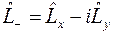Простой проверкой можно убедиться в справедливости соотношений

, , .

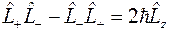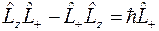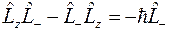Далее, вычисляя оператор квадрата углового момента, получим

,

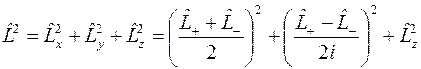или

.

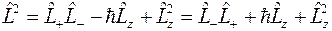Рассмотрим состояние, в котором проекция углового момента на ось z принимает наибольшее значение

.

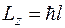В этом состоянии

, .

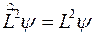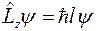Из соотношений коммутации для такой функции получим

.

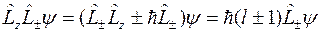Отсюда следует, что функци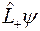и и 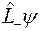являются собственными функциями оператора 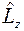, имеющими собственные значения 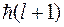и 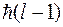, соответственно. Но величина 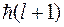не может быть собственным значением оператора 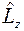, так как по предположению наибольшим собственным значением этого оператора является .

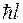Таким образом, равенство

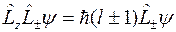
невозможно, хотя оно логически вытекает из соотношений коммутации и уравнения .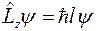

Избежать противоречия можно только в том случае, если 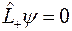. Но отсюда следует 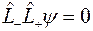и

.

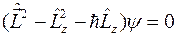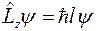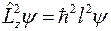Но в силу того, что и , получим

.

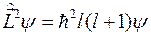Следовательно, собственные значения оператора углового момента равны

.

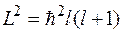Квантовое число 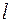называется орбитальным квантовым числом и принимает положительные целочисленные значения 0, 1, 2, ….

Состояния микрочастицы с заданным значением квадрата углового момента 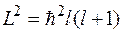могут иметь различные проекции углового момента на выделенное направление, в которых магнитное квантовое число может принимать 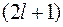значений: 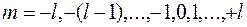. Данные результаты, определяющие возможные значения 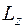и 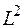, называют пространственным квантованием.

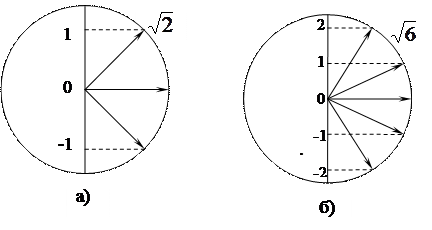
Для наглядности пространственное квантование обычно представляют на векторных диаграммах. По оси z откладывают возможные значения m, рассматривая их как проекции вектора 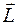длины 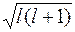, имеющего дискретные направления в пространстве. Эти диаграммы не следует понимать буквально. (Вектор углового момента в квантовой механике принципиально не имеет определенных направлений в пространстве.) Они правильно передают только два факта: возможные значения проекции m и возможные значения квадрата углового момента .

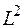В классической механике кинетическая энергия вращающегося тела определяется формулой

,

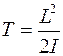где 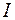- момент инерции тела относительно соответствующей оси вращения. Такая же формула справедлива и в квантовой механике. Различие состоит в том, что величина 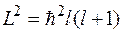принимает дискретные значения.

Неизменяемая вращающаяся система в квантовой механике называется ротатором. Таким образом, энергетические уровни ротатора дискретны и определяются формулой

.

Для некоторых целей вращающуюся молекулу можно рассматривать как жесткий ротатор, и пользоваться этой формулой, если изменения l, связанные с вращением, не велики.

Дата добавления: 2014-11-29