Модель гармонического осциллятора

Зависимость энергии взаимодействия двух атомов от расстояния между ними показана на рис.. При некотором расстоянии она имеет минимальное значение. Положив реальную зависимость энергии взаимодействия в окрестности этой точки можно представить в виде ряда Тейлора

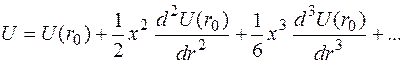
Для малых колебаний достаточно ограничиться первыми двумя членами. Кроме того, выбором начала отсчета энергии первое слагаемое можно обратить в нуль. В результате зависимость энергии взаимодействия атомов можно аппроксимировать параболической зависимостью

,

где

Такая аппроксимация приводит к модели гармонического осциллятора. В классической механике она описывает движение квазичастицы с приведенной массой , взаимодействующей с неподвижным силовым центром. При этом частота колебаний .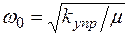

Гармонический осциллятор в механике является идеализацией, так как зависимость потенциальной энергии 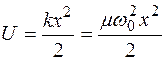означает, что потенциальная энергия неограниченно возрастает при увеличении расстояния 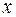. Во всех реальных ситуациях, начиная с некоторых значений амплитуды, начинаются значительные отклонения от гармоничности, а при больших значениях 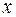сила взаимодействия стремится к нулю. Однако для небольших амплитуд колебаний вполне можно пользоваться представлением о гармонических колебаниях.

Колебательные процессы очень распространены в природе, в том числе и в различных атомных системах: колебания атомов в молекулах, или в кристаллах. В многоатомных системах в линейном приближении можно ввести систему обобщенных координат, в которых уравнения движения разделяются, и сложное движение атомов заменяется колебательным движением системы квазичастиц - гармонических осцилляторов. При увеличении амплитуды колебания становятся нелинейными, а система независимых осцилляторов становится системой связанных осцилляторов.

Приведенные примеры показывают, что квантовомеханическое рассмотрение гармонического осциллятора представляет интерес для изучения физики молекул и физики твердого тела.

Функция Гамильтона для классического одномерного гармонического осциллятора имеет вид

.

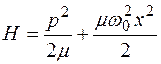Соответствующий гамильтониан приводит к изучению одномерного движения микрочастиц в бесконечной параболической яме.

Уравнение Шредингера в этом случае имеет вид

.

Дата добавления: 2014-11-29