Одномерного гармонического осциллятора

Собственные значения и собственные функции

Освободившись от множителя перед второй производной, получим уравнение

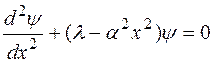, (1)

где

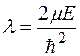, . (2)

Точка 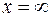является особой точкой уравнения. Поэтому решение этого уравнения ищут в виде

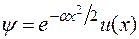. (3)

Первый множитель такого решения устраняет из уравнения член 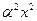. А для функции 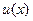получается уравнение

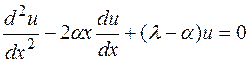. (4)

Отрицательный показатель экспоненты обеспечивает конечность волновой функции на бесконечности.

Введя безразмерную переменную

, (6)

уравнение (4) преобразуем к виду

. (7)

Решением этого уравнения будет 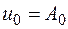. В этом случае параметр 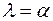, а волновая функция

.

Это решение не имеет узлов, поэтому оно описывает основное состояние гармонического осциллятора. Ему соответствует нулевая энергия

.

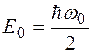Решением уравнения (7) будет также .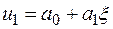

Действительно подстановка этого решения в (7) дает

.

Приравнивая нулю коэффициенты при разных степенях 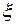, получим

, .

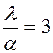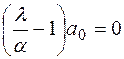Таким образом,

, .

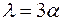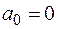Поэтому

, .

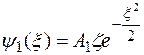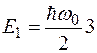Волновая функция первого возбужденного состояния имеет один узел и его энергия больше нулевой энергии на .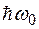

В стационарном состоянии с энергией 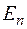функция

должна иметь 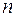узлов. Это значит, что функция 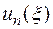должна быть полиномом 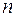-й степени с некратными корнями. Эти полиномы называются полиномами Эрмита-Чебышева

.

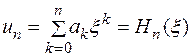Они являются решением уравнения (7)

.

Это уравнение должно выполняться при любых 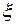, т.е. коэффициенты при одинаковых степенях должны обращаться в нуль. Для определения собственных значений уравнения достаточно приравнять нулю коэффициент при старшей степени

.

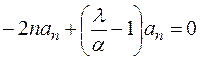Отсюда находим или

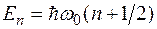. (8)

При этом полиномы Эрмита-Чебышева должны удовлетворять уравнению

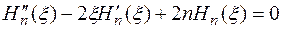. (9)

Из условия (8) следует, что собственные значения уравнения Шредингера для гармонического осциллятора принимают дискретный ряд значений.

Энергетические уровни гармонического осциллятора расположены на одинаковых расстояниях друг от друга

.

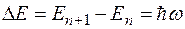Наименьшая энергия, которую имеет гармонический осциллятор – энергия нулевых колебаний

.

Наличие энергии нулевых колебаний находится в полном соответствии с принципом неопределенностей Гейзенберга: микрочастица никогда не может остановиться и иметь одновременно точное значение координаты 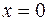и импульса .

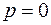Таким образом, теория Шредингера подтвердила правильность предположения Планка об эквидистантности значений энергии осцилляторов поля и о величине кванта энергии. Кроме того, квантовая теория предсказывает существование нулевых колебаний осциллятора, что соответствует принципу неопределенностей.

Решение уравнения (9) можно записать в виде

.

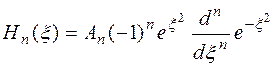Множитель здесь введен для того, чтобы сделать положительным коэффициент при старшей степени положительным. Нормировочный множитель 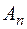определяется из условия нормировки волновых функций и выражается формулой

.

Нормированный полином Эрмита-Чебышева описывается формулой

.

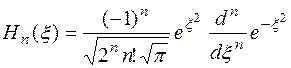Выпишем несколько первых полиномов Эрмита-Чебышева

,

,

,

.

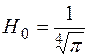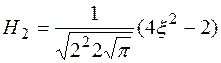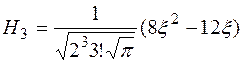Нормированные волновые функции Эрмита разных состояний

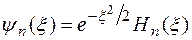
ортогональны.

Дата добавления: 2014-11-29