Микрочастица в одномерной прямоугольной потенциальной яме

1. Рассмотрим сначала одномерное движение микрочастицы, причем будем считать, что в области потенциальная энергия равна нулю, а за ее пределами обращается в бесконечность (рис. 3). В этом случае вероятность нахождения микрочастицы за пределами ямы равна нулю и волновая функция обращается в нуль на краях области движения (пр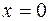и и 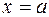). В одномерной задаче волновая функция зависит только от координаты x. Поэтому в операторе Лапласа используется только дифференцирование по одной переменной и стационарное уравнение Шредингера является обыкновенным дифференциальным уравнением второго порядка

, (84)

.

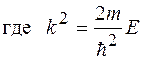Общее решение такого уравнения содержит две произвольные постоянные A и B

,

которые определяются из дополнительных условий.

Из граничного условия на левой границе

следует .

Граничное условие на правой границе

выполняется не для любых значений волнового числа k, а только для квантованных, удовлетворяющих условию

, где

Это условие квантования позволяет найти собственные функции уравнения Шредингера (84)

(85)

и собственные значения

. (86)

Постоянная В определяется из условия нормировки волновых функций

и равна

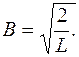
Графики собственных функций изображены на рис. 39. На рис. 40 показано распределение плотности вероятности обнаружения частицы на различных расстояниях от стенок ямы, равная . Из графиков, например, следует, что в состоянии с n =2 частица не может быть обнаружена в середине ямы и вместе с тем одинаково часто бывает как в левой, так и в правой половине ямы. Такое поведение частицы, очевидно, несовместимо с представлением о траекториях. Согласно классическим представлениям все положения частицы в яме равновероятны.

2. Мы решили очень упрощенную задачу, но, тем не менее, она охватывает очень многие особенности поведения микрочастиц в реальных системах.

Во-первых, отметим, что квантование энергии получается при решении уравнения Шредингера автоматически без введения дополнительных постулатов. В данной конкретной задаче это квантование означает, что в пределах бесконечно глубокой прямоугольной потенциальной ямы должно укладываться целое количество длин полуволн де Бройля. В этом смысле задача математически эквивалентна задаче о колебаниях закрепленной струны.

В самом нижнем энергетическом состоянии (n = 1) энергия микрочастицы

отлична от нуля, что соответствует принципу неопределенностей Гейзенберга. Даже в самом нижнем энергетическом состоянии микрочастица не может остановиться (иметь нулевой импульс и определенную координату), и энергию этого состояния называют нулевой энергией.

Во-вторых, расстояние между энергетическими уровнями

и его относительная величина

позволяет сформулировать выводы общие для многих квантовых систем (задач).

Прежде всего, отметим, что относительная величина квантования энергии уменьшается с ростом квантового числа n. То есть для более высоких состояний роль квантования понижается: D < < .

Затем отметим, что величина квантов энергии D тем меньше, чем больше масса частицы и чем больше область ее движения.

Так для молекулы массой m = 10^{-26 кг} , двигающейся в сосуде размером 0,1 м величина квантов энергии

настолько мала (например, по сравнению с тепловой энергией при комнатной температуре

что энергетический спектр молекулы можно считать квазинепрерывным.

Точно также для электрона (m = 10^{-31 кг} ) в кристалле (L = 10^{-3 м} )

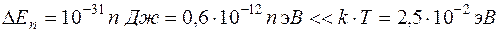
энергетический спектр также можно считать квазинепрерывным.

Но если область движения электрона порядка атомных размеров (), то энергетический интервал между соседними уровнями

настолько велик по сравнению с тепловой энергией, что не учитывать дискретность энергетических уровней уже нельзя.

Дата добавления: 2014-11-29