Момент импульса

1. Согласно классическому определению моментом импульса 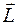частицы относительно начала координат О называется величина, равная векторному произведению радиус-вектора материальной точки 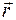и ее импульса

.

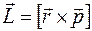В квантовой механике не существует состояния, в котором оба вектора 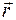и имеют определенные значения. Это накладывает отпечаток на свойства оператора момента импульса

.

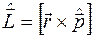Используя представление операторов 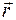и 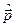в декартовых и сферических координатах

,

,

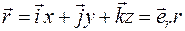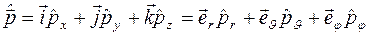и соблюдая порядок расположения операторов и координат и проекций импульса, с помощью записи векторного произведения в форме определителя

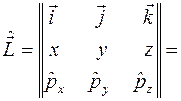
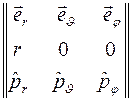
можно получить разложение оператора 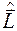на составляющие

;

.

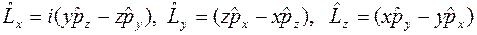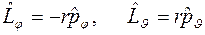Оператор вектора момента импульса выражается через свои проекции формулой

.

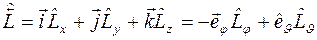Произвольной волновой функции 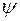соответствует вектор, определяемый выражением

.

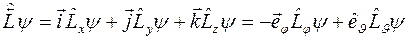Возникает, однако, вопрос, существует ли такая волновая функция 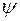, для которой все три проекции этого вектора имеют определенные значения, т.е. одновременно выполняются все три равенства:

, , .

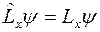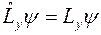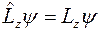Для ответа на этот вопрос необходимо найти правила коммутации операторов .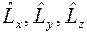

2. Коммутационные соотношения проверяются непосредственным перемножением операторов

,

.

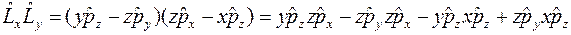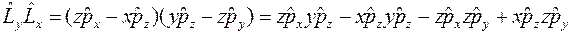Таким образом,

.

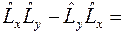
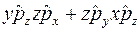
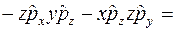
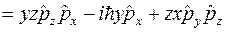
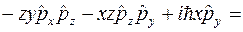
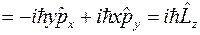Аналогично получаются и два других правила коммутации.

Итак,

, , .

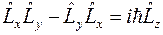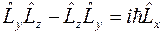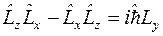Любые две проекции оператора момента не коммутируют между собой. Поэтому не существует состояния, в котором бы все три и даже какие либо две из трех проекций 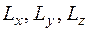имели определенные значения. Исключением является только случай, когда все три проекции одновременно равны нулю. Значит, не существует состояния, в котором бы и сам вектор момента импульса имел определенное значение, т.е. был бы определен полностью как по величине, так и по направлению.

Другими словами оператор момента импульса не имеет собственных значений и собственных функций.

В квантовой механике используются операторы проекций момента импульса на оси координат и квадрата момента импульса .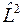

Можно убедиться проверкой, что операторы проекций момента импульса коммутируют с оператором квадрата момента

, , .

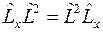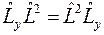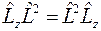Таким образом, в состоянии, в котором 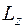имеет определенное значение, две другие проекции не имеют определенного значения, но квадрат момента импульса имеет определенное значение. Поэтому 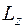и 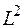могут быть измерены одновременно.

3. В дальнейшем понадобятся выражения для оператора проекции момента импульса на ось z, записанные в сферических координатах

,

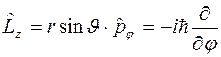и квадрата момента импульса в сферических координатах

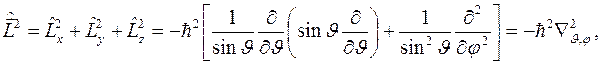
где 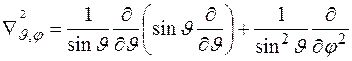- оператор Лапласа на сфере.

Оператор момента импульса от выбора начала координат не зависит, а зависит только от направления координатных осей. Поэтому в квантовой механике его называют оператором углового или вращательного момента микрочастицы. Не зависят от выбора начала системы отсчета и собственные значения операторов проекций и квадрата углового момента.

Дата добавления: 2014-11-29