
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Собственные функции оператора квадрата момента импульса
|
|
|
|
Уравнение для определения собственных функций и собственных значений оператора  имеет вид
имеет вид
 .
.
Введя обозначение
 ,
,
и записывая оператор Лапласа на сфере в явном виде, получим дифференциальное уравнение в частных производных
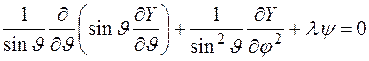 . (1)
. (1)
Уравнение необходимо решить для всей области координат на сфере ( ,
,  ). Поэтому собственные функции оператора квадрата момента импульса зависят только от угловых координат. Они называются сферическими функциями и используются в различных разделах физики (в акустике, электродинамике, метеорологии, и т.д.). Так как собственные функции операторов квадрата момента и проекции момента на ось
). Поэтому собственные функции оператора квадрата момента импульса зависят только от угловых координат. Они называются сферическими функциями и используются в различных разделах физики (в акустике, электродинамике, метеорологии, и т.д.). Так как собственные функции операторов квадрата момента и проекции момента на ось 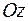 являются общими, то решение этого уравнения отыскивается методом разделения переменных, полагая
являются общими, то решение этого уравнения отыскивается методом разделения переменных, полагая
 .
.
Подстановка этого решения в уравнение, приводит к выражению
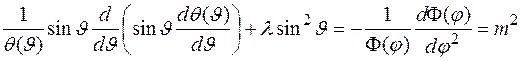
В этом выражении приравниваются функции, зависящие от разных аргументов, что возможно, если они равны постоянной величине, которую мы обозначили  . В результате разделения переменных мы получили два обыкновенных дифференциальных уравнения
. В результате разделения переменных мы получили два обыкновенных дифференциальных уравнения
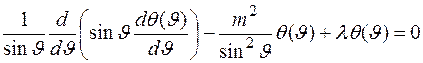 , (2)
, (2)
 . (3)
. (3)
Волновая функция оператора проекции момента импульса удовлетворяет уравнению (3).
Уравнение (2) имеет непрерывные однозначные конечные решения только при строго определенных значениях параметра
 ,
, 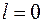 , 1, 2, 3,....
, 1, 2, 3,....
Это значит, что квадрат момента импульса принимает дискретный ряд значений
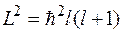 .
.
Отметим только, что решения уравнения (2) зависят от двух чисел 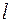 и
и 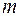 . Сделав замену переменной
. Сделав замену переменной 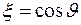 в уравнении, его решения представляют собой присоединенные полиномы Лежандра.
в уравнении, его решения представляют собой присоединенные полиномы Лежандра.
 ,
,
где

- полиномы Лежандра
Процедура решения уравнения (2) выходит за рамки курса общей физики. Поэтому мы ограничимся приведением сферических волновых функций 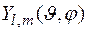 для нескольких небольших квантовых чисел
для нескольких небольших квантовых чисел
 ,
,
 ,
,  ,
, 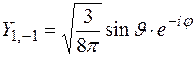 ,
,
 ,
,  ,
, 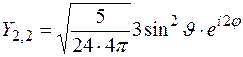 .
.
Сферические волновые функции позволяют определить вероятность того, что микрочастица (квазичастица), находящаяся в состоянии, описываемом волновой функцией  , будет находиться в элементе телесного угла
, будет находиться в элементе телесного угла 
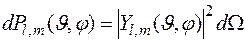 .
.
Поэтому эта вероятность не зависит от угла 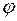 . Это означает, что в плоскости, перпендикулярной оси
. Это означает, что в плоскости, перпендикулярной оси 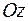 распределение вероятности имеет осевую симметрию.
распределение вероятности имеет осевую симметрию.
Угловое распределение вероятности зависит от квантовых чисел 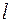 и
и 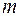 , т.е. от величины момента импульса и величины его проекции на ось
, т.е. от величины момента импульса и величины его проекции на ось 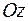 .
.

Состояние с 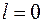 (
(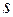 -состояние) обладает сферической симметрией распределения вероятности, так как
-состояние) обладает сферической симметрией распределения вероятности, так как  . Поэтому
. Поэтому
 .
.
Такие состояния являются сферически симметричными и обозначаются буквой s.
Для l = 1 состояния с различными значениями магнитного квантового числа имеют различную направленность в угловом распределении плотности вероятности. Такие состояния обозначаются буквой p.
 ,
,  .
.
Для l =2 число состояний увеличивается до пяти и направленность электронных облаков увеличивается (лепестки распределений сужаются).
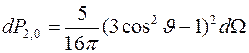 ,
, 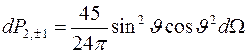 ,
,
 .
.
Соответствующие распределения угловой плотности вероятности показаны на рисунке.
Состояния с l =2,3,4,... обозначаются буквами d, f, g,.., соответственно.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1057; Нарушение авторских прав?; Мы поможем в написании вашей работы!