
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные определения. Способы задания множеств
|
|
|
|
Способы задания множеств
Понятие множества
Множества и операции над ними
Теория множеств опирается на три первичных понятия:
1) множество;
2) элемент;
3) принадлежность.
Строгого определения этим понятиям не дается, описывается только их применение. Для этих понятий используются обозначения: “ 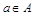 ”- элемент а принадлежит множеству А; “
”- элемент а принадлежит множеству А; “ 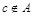 ”элемент с не принадлежит множеству А.
”элемент с не принадлежит множеству А.
Говоря о некотором множестве, мы требуем его:
1) целостности, т.е. возможности рассматривать его как отдельный объект;
2) различимости его элементов;
3) неупорядоченности элементов.
Поэтому записи  и
и 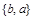 определяют одно и то же множество.
определяют одно и то же множество.
Множество можно задать, перечислив все его элементы: 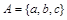 ,
, 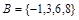 . Порядок записи элементов множества произволен. Часто задают множество, указав его характеристическое свойство, которое для каждого элемента позволяет выяснить, принадлежит он множеству или нет.
. Порядок записи элементов множества произволен. Часто задают множество, указав его характеристическое свойство, которое для каждого элемента позволяет выяснить, принадлежит он множеству или нет.
Например,
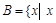 – целый корень уравнения
– целый корень уравнения 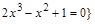 ,
,
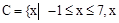 – целое }.
– целое }.
В дальнейшем для известных числовых множеств будут использоваться обозначения:
N = { 1,2,3,…} – множество натуральных чисел;
Z = { …, -2,-1,0,1,2,…} – множество целых чисел;
Q – множество рациональных чисел;
R – множество действительных чисел.
Пустым множеством называется множество Æ, не содержащее ни одного элемента, т.е. для любого элемента x выполняется 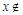 Æ.
Æ.
Универсальным называется множество U всех элементов, рассматриваемых в данной задаче.
Пример. Пусть U = Z и требуется найти все решения уравнения 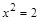 . Множество М решений этой задачи есть пустое множество: М = Æ.
. Множество М решений этой задачи есть пустое множество: М = Æ.
Пусть теперь U = R. Тогда множество М решений уравнения 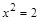 не пусто: М =
не пусто: М = 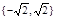 .
.
Будем говорить, что множество А включается во множество В 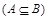 , если каждый элемент множества А является элементом множества В (говорят также, что А является подмножеством множества В). Из определения включения следуют свойства:
, если каждый элемент множества А является элементом множества В (говорят также, что А является подмножеством множества В). Из определения включения следуют свойства:
1) 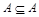 для любого множества А;
для любого множества А;
2) Если 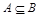 и
и 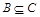 , то
, то 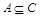 ;
;
3) Æ 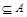 для любого множества А;
для любого множества А;
4)  U для любого множества А.
U для любого множества А.
Подмножество 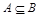 называется собственным подмножеством множества В (
называется собственным подмножеством множества В (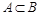 - строгое включение), если А не пусто и не совпадает с В. Например, имеют место строгие включения: N
- строгое включение), если А не пусто и не совпадает с В. Например, имеют место строгие включения: N 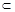 Z
Z 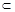 Q
Q 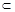 R.
R.
Определим понятие равенства множеств: А=В тогда и только тогда, когда одновременно выполняются два включения 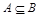 и
и 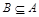 , т.е. каждый элемент множества А является элементом множества В и каждый элемент множества В является элементом множества А:
, т.е. каждый элемент множества А является элементом множества В и каждый элемент множества В является элементом множества А:
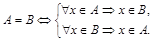
Свойства равенства множеств:
1) для любого А справедливо А=A;
2) если А=В, то и В=A;
3) если А=В и В=C, то A=C.
1.1.4. Диаграммы Эйлера – Венна
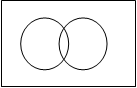
Эти диаграммы применяются для наглядного изображения множеств и их взаимного расположения.
 |
U
A B
Рис. 1.1 Диаграмма Эйлера-Венна
Универсальное множество U изображается в виде прямоугольника, а произвольные множества – подмножества универсального – в виде кругов (рис. 1.1).
При этом возможны следующие случаи взаимного расположения двух множеств А и В:
1) одно из множеств строго включается в другое (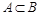 или
или 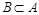 );
);
2) множества равны;
3) множества не имеют общих элементов;
4) множества находятся в общем положении, т.е. не подходит ни один из вышеперечисленных случаев, и множества расположены как на рис. 1.1.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 475; Нарушение авторских прав?; Мы поможем в написании вашей работы!