Преобразование уравнений состояния

Пусть система описывается уравнениями состояния общего вида (8.3). Сделаем в этих уравнениях замену переменных x = Q z, где – новый вектор состояния, Q – произвольная матрица размерностью с постоянными коэффициентами. На матрицу Q накладывается единственное ограничение – она должна быть невырожденной (неособенной), т.е. определитель этой матрицы . В этом случае всегда существует обратная матрица, которую будем обозначать через , такая, что , где – единичная матрица размерностью . Очевидно, что при этих условиях существует однозначная связь между векторами x и z: , .

В уравнениях (8.3) сделаем замену x = Q z и с учетом того, что , получим

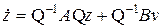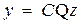, . (8.8)

Уравнения (8.8) будут новыми уравнениями состояния, имеющими основную матрицу системы , входа и выхода C Q. Так как Q – произвольная матрица, то исходным уравнениям (8.3) соответствует бесчисленное количество эквивалентных уравнений состояния (8.8).

Отметим, что две матрицы A и 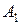, связанные преобразованием , называются подобными. Подобные матрицы имеют одинаковые собственные значения.

Используя линейное преобразование, можно поставить задачу о выборе при исследовании той или иной формы уравнений состояния. Наиболее часто решается задача преобразования исходной системы (8.3) к нормальной или канонической форме уравнений состояния (8.8).

Доказано, что для произвольной матрицы А всегда существует невырожденная квадратная матрица размерностью , которую обозначим через M и назовем модальной, такая, что матрица будет иметь форму Жордана. Если матрица А имеет различные собственные значения (числа) , являющиеся корнями характеристического уравнения

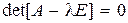, (8.9)

то матрица будет диагональной: .

Таким образом, преобразование произвольной системы уравнений (8.3) к канонической форме всегда возможно. Наиболее просто задача определения модальной матрицы решается для случая различных собственных чисел матрицы А, которые обозначим через . Для каждого собственного числа находится собственный вектор 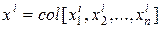из решения векторно-матричного уравнения

. (8.10)

Матрица, образованная вектор-столбцами , т.е. матрица

, (8.11)

и будет искомой модальной матрицей.

В соответствии с (8.9) при 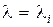определитель системы линейных уравнений (8.10) равен нулю, т.е. система имеет бесчисленное множество решений, каждое из которых можно принять за собственный вектор. Отсюда матрица М является неединственной.

В случае кратных собственных значений матрицы А задача определения модальной матрица значительно усложняется.

В частности, если исходная матрица А является матрицей Фробениуса
вида

(8.12)

и собственные числа , являющиеся корнями характеристического уравнения

= 0, (8.13)

различны, то модальная матрица будет иметь вид

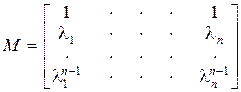. (8.14)

Пример 8.3. Пусть в САУ, которая рассматривалась в примерах 8.1 и 8.2, с, , тогда уравнения (8.7) будут иметь вид

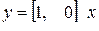, . (8.15)

Преобразуем уравнения состояния к канонической форме. Основная матрица системы А является матрицей Фробениуса. Найдем ее собственные значения из решения характеристического уравнения

.

Корни уравнения будут различными: 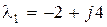, . Таким образом, в соответствии с (8.14) определяем модальную матрицу M и обратную ей :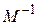

, .

Далее M ^–1 AM = diag [–2+ j 4, –2 – j 4], , .

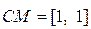Итак, уравнения состояния (8.15) преобразуются к канонической форме:

, .

Пример 8.4. Пусть система описывается уравнениями состояния

, .

Корни характеристического уравнения будут , .

Находим собственные векторы из решения системы линейных уравнений , .

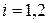Полагая , будем иметь

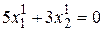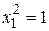Из последних двух уравнений , откуда, задавая, например, , получим . Итак, первый собственный вектор . При в конечном итоге для определения координат второго собственного вектора получим . Полагая , будем иметь и соответственно . Итак, матрицу М можно выбрать в виде

, .

, , .

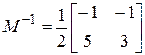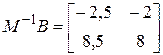Окончательно уравнения в канонической форме будут иметь следующий вид:

, .

Дата добавления: 2014-12-07