Каноническая форма уравнений состояния одномерной системы

Для получения уравнений состояния одномерной системы в канонической форме используется передаточная функция системы. Будем полагать, что система описывается дифференциальным уравнением (8.16), которому соответствует передаточная функция .

Пусть характеристическое уравнение системы имеет n различных корней , тогда передаточную функцию можно представить в виде

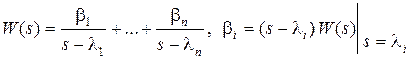. (8.22)

Очевидно, что в этом случае .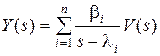

Обозначим , тогда , .

Перейдем в операторных соотношениях к оригиналам, полагая . Получим , , .

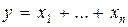Вводя вектор состояния 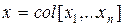, запишем полученные уравнения в виде уравнений состояния

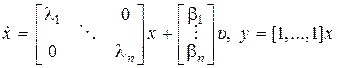. (8.23)

Итак, получили уравнения состояния в канонической форме с диагональной матрицей коэффициентов, где в общем случае элементы , 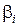матриц могут быть и комплексными величинами.

Из (8.22) можно получить другую каноническую форму уравнений состояния. Если обозначить 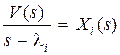, то проводя аналогичные рассуждения, получим уравнения состояния:

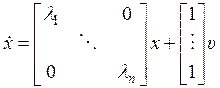, . (8.24)

Рассмотрим теперь случай кратных корней. Пусть характеристическое уравнение имеет корни 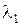кратности k, а остальные корни 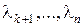простые.

Тогда передаточную функцию можно представить в виде разложения

,

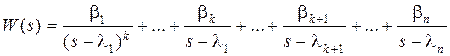где ,

.

в этом случае 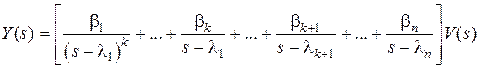или .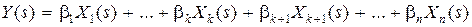

Между изображениями 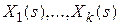существует связь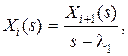 . Полагая и переходя к оригиналам, получим в области оригиналов: ; ; ; .

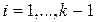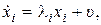
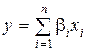Вводя вектор состояния 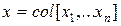, полученные соотношения запишем в векторно-матричной форме:

(8.25)

Уравнения состояния (8.25) имеют каноническую форму, основная матрица – форму Жордана. Корню кратности k соответствует клетка Жордана размерностью . Очевидно, при наличии нескольких кратных корней будем получать соответствующие клетки Жордана для каждого корня.

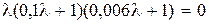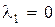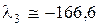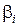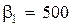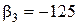Пример 8.6. Обратимся к системе управления из примера 8.5 и найдем уравнения состояния в канонической форме для разомкнутой системы. Характеристическое уравнение разомкнутой системы имеет три различных корня: , , . Используя выражение , находим величины : , , . Таким образом, уравнения состояния в канонической форме для разомкнутой системы имеют вид

, .

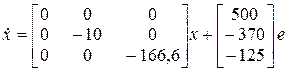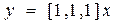С учетом уравнения замыкания нетрудно получить следующие уравнения состояния замкнутой системы:

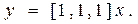, (8.26)

Сравнивая (8.21) и (8.26), видим, что одна и та же система описывается разными уравнениями состояния, которые эквивалентны между собой.

Дата добавления: 2014-12-07