Устойчивость, управляемость и наблюдаемость линейных систем

Рассмотрим линейную систему, описываемую уравнениями состояния (8.27). Устойчивость процессов в системе можно рассматривать по отношению к тем или иным переменным, характеризующим систему. Очевидно, из (8.27) следует, что поведение системы можно рассматривать по отношению к переменным состояния (вектору состояния x) или к выходным переменным (вектору выхода y). процессы в системе могут быть устойчивы по отношению к одной группе переменных и неустойчивы по отношению к другой. Чаще всего рассматривают устойчивость по отношению к переменным состояния x (t). за исключением особых случаев это будет справедливо и по отношению к вектору выхода y.

Закон изменения вектора состояния x (t) определяется выражением (8.32). В случае линейной системы устойчивость процессов в ней зависит только от поведения свободной составляющей 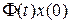, обусловленной начальным значением вектора состояния, т.е. составляющей

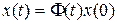. (8.41)

Пусть корни характеристического уравнения системы

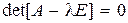, (8.42)

соответствующего системе (8.27), будут все различные , тогда переходная матрица состояния 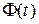представима в виде (8.34), где М – модальная матрица, элементы которой не зависят от времени. В этом случае (8.41) запишем в виде

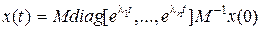. (8.43)

Процессы в системе автоматического управления по отношению к переменным состояния будут асимптотически устойчивы, если при любом начальном значении x (0) свободная составляющая (8.43) с течением времени затухает, т.е. 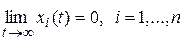. Процессы в системе будут просто устойчивы, если , неустойчивы, если хотя бы для одной координаты .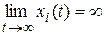

В соответствии с тремя рассматриваемыми случаями будем говорить об асимптотически устойчивой, устойчивой (нейтральной или находящейся на границе устойчивости) и неустойчивой линейных системах.

Из приведенных определений и анализа выражения (8.43) следует, что система будет асимптотически устойчивой, если все действительные части корней строго отрицательны, т.е. . Система будет просто устойчивой, если 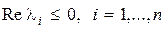, и неустойчивой, если для некоторого корня .

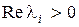Наличие кратных корней не меняет полученных результатов относительно асимптотической устойчивости и неустойчивости.

Таким образом, необходимым и достаточным условием асимптотической устойчивости системы (8.27) является отрицательность действительных частей всех корней характеристического уравнения (8.42), т.е. все .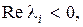

Если в (8.42) раскрыть определитель, то в результате получим уравнение , где 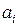определяются через элемент 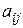матрицы А.

К последнему уравнению обычным путем можно применить известные критерии устойчивости (Гурвица, Рауса, Михайлова и т.п.).

Прежде чем сформулировать в общем виде понятия, связанные с управляемостью и наблюдаемостью систем, рассмотрим частный случай. Пусть система управления с одним входом и одним выходом описывается уравнениями состояния

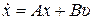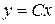, , (8.44)

где А – 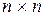матрица; ; , , .

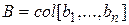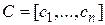Предположим, что матрица А имеет различные собственные значения 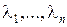. Сделаем в (8.44) замену x = Mz, где M – модальная матрица
размерностью 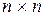. В результате приходим к канонической форме уравнений состояния

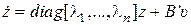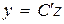, , (8.45)

где , , , .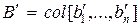

Скалярный элемент получается перемножением i -й строки матрицы 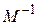на столбец В, а элемент 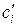– перемножением строки С на i -ю строку матрицы М.

Уравнения (8.45) запишем в скалярном виде:

. (8.46)

На рис. 8.5 по уравнениям (8.46) построена схема моделирования.

υ

Рис. 8.5

Из этого рисунка следует, что внутренняя структура системы представляет параллельное соединение n однотипных ветвей, соответствующих каждому характеристическому числу.

Если все отличны от нуля, то с помощью входного сигнала 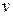можно влиять на все координаты 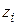(управлять ими). Однако при определенных условиях в зависимости от значений элементов матриц 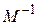и В могут возникнуть случаи, когда один или несколько коэффициентов будут равны нулю. Тогда одна или несколько координат 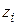не будут зависеть от входного сигнала 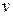, не будут им управляться, т.е. соответствующая цепь оказывается разорванной по входу.

Аналогичная картина может наблюдаться по отношению к выходу y. Если все 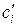отличны от нуля, то в выходном сигнале присутствуют (наблюдаются) все координаты 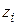. Если же один или несколько коэффициентов 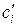равны нулю, то соответствующие переменные состояния не могут быть измерены или не наблюдаются. В данном случае имеем разрыв во внутренней структуре системы на выходе соответствующих цепей.

Из рассмотренного примера, в частности, следует, что система, описываемая уравнениями (8.44), будет полностью управляемой и полностью
наблюдаемой, если все элементы матриц 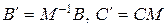будут отличны от нуля.

Коэффициенты определяются коэффициентами матрицы В и собственными числами матрицы А, т.е. фактически коэффициентами матрицы А. Отсюда следует, что управляемость системы зависит только от пары матриц А и В. Аналогично наблюдаемость будет зависеть от пары матриц А и С.

Если система полностью управляема и наблюдаема, то порядок передаточной функции системы будет совпадать с порядком дифференциального уравнения в (8.44) и будет равен n. В случае неполной управляемости или наблюдаемости порядок передаточной функции будет меньше, чем n. Этот результат следует из структуры (см. рис. 8.5), так как в этом случае в части каналов нет связи между 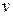и y. Например, если или 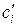равны нулю, то порядок передаточной функции будет (n – 1), хотя порядок системы (8.44) равен n. Отсюда следует, что передаточная функция характеризует только полностью управляемую и наблюдаемую часть системы.

Рассмотрим теперь свойства устойчивости системы в связи с ее управляемостью и наблюдаемостью. Пусть, например, 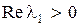, а все остальные 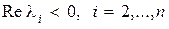. В этом случае по отношению к координатам (то же самое 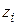) система неустойчива. Если в этом случае система не наблюдаема по координате , то 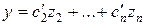и неустойчивая координата не влияет на выход системы. по отношению к выходу система будет вести себя как устойчивая. Отсюда следует, что если система полностью наблюдаема, то устойчивость по отношению к переменным состояния (иногда ее называют внутренней устойчивостью) будет совпадать с устойчивостью по отношению к выходной координате (внешней устойчивостью). В случае ненаблюдаемой системы это условие может не выполняться.

Будем полагать, что уравнения (8.44) описывают объект управления. Регулятор, управляющий этим объектом (выход регулятора – это сигнал 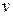), формирует сигнал управления, используя выходной сигнал y. Пусть объект управления является неустойчивым 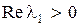и неуправляемым по координате , тогда какой бы регулятор мы ни применили, с помощью обратной связи и регулятора невозможно сделать систему устойчивой, так как разорвана на входе первая цепь. Говорят, что в этом случае объект является нестабилизируемым.

Дадим более строгие определения управляемости и наблюдаемости линейной системы (8.44) общего вида, т.е. в (8.44) будем полагать , , – матрицы соответствующих размерностей. Обозначим значения вектора состояния 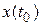при , при , .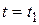

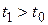Система (8.44) называется полностью управляемой, если для любых моментов времени и 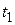и любых заданных состояни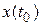й и существует управление 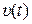(), переводящее начальное состояние 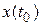в конечное .

Состояние 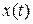системы (8.44) называется наблюдаемым, если в момент наблюдения 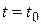можно однозначно определить по данным измерения и 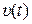на конечном интервале времени , 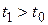. Система (8.44) называется полностью наблюдаемой, если наблюдаемы все ее состояния в любые моменты времени.

Американским ученым Р. Калманом были предложены критерии
управляемости и наблюдаемости. Вводятся в рассмотрение матрица управляемости 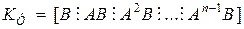и матрица наблюдаемости .

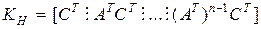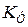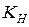Матрица имеет размерность , а матрица – размерность , символ т означает операцию транспортирования матрицы.

Столбцами матрицы 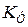являются столбцы матриц В, . Аналогично столбцы матрицы 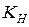– это столбцы матриц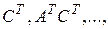 . Если уравнения (8.44) описывают одномерную систему, то 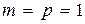и
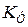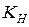, будут квадратными матрицами размерности .

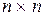Критерий управляемости и наблюдаемости. Система (8.44) является полностью управляемой только тогда, когда ранг матрицы управляемости равен n, и полностью наблюдаемой только тогда, когда ранг матрицы наблюдаемости равен n.

Напомним, что под рангом матрицы понимается максимальный порядок ее минора, отличного от нуля.

Пример 8.9. Рассмотрим одномерную систему второго порядка

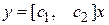, . (8.47)

Основная матрица системы А является сопровождающей. Предположим, что ее собственные числа , являющиеся корнями уравнения 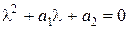, различны (следовательно ). Приведем систему к канонической форме с помощью преобразования , . В результате

, ,

где , , , .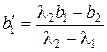

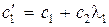По уравнениям (8.47) найдем передаточную функцию системы

Пусть , , 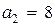, 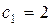. Очевидно, , , 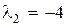, 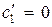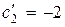. Система является ненаблюдаемой по координате 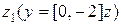. Подстановка значений коэффициентов в передаточную функцию дает

, (8.48)

т.е. передаточная функция 2-гo порядка вырождается в передаточную функцию 1-го порядка.

Если выбрать, например, 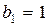, , , , 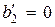то система будет неуправляема по второй координате .

Таким образом, система с уравнениями состояния

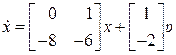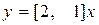, (8.49)

является неуправляемой по одной из внутренних координат и ненаблюдаемой по другой. При этом передаточная функция (8.48) при 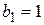, вообще вырождается в нулевую 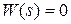и между переменными 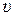и y отсутствует всякая связь. Очевидно, по виду уравнения (8.49) трудно было бы предвидеть такие результаты.

К (8.49) применим критерий управляемости и наблюдаемости

, .

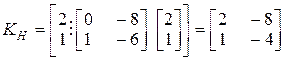Ранг обеих матриц меньше двух (равен единице). Система не полностью управляема и не полностью наблюдаема.

Дата добавления: 2014-12-07