Передаточная и весовая матрицы

Наряду с переходной матрицей состояния при описании и исследовании линейных многомерных систем находят применение матричные аналоги обычных передаточных функций одномерных систем.

Применим к уравнениям (8.27) преобразование Лапласа, полагая x (0) = 0, тогда получим , 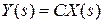или, исключая из уравнений вектор 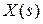, получим

. (8.38)

Передаточной матрицей (матричной передаточной функцией) 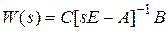будем называть матрицу размерности 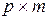, связывающую изображение вектора входа 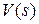и вектора выхода .

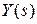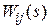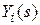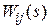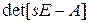Элементами передаточной матрицы являются обычные скалярные передаточные функции, связывающие i -й выход с j -м входом при условии, что все остальные входы равны нулю. Передаточная функция есть отношение двух полиномов относительно s. Полином знаменателя является для всех одним и тем же и равен (степень его n), а полиномы числителя будут степени не выше (n – 1).

В уравнении (8.33) будем полагать 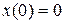. Внесем матрицу С под знак интеграла и запишем это уравнение в виде

. (8.39)

Матрицу 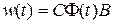размерностью будем называть весовой матрицей (импульсной переходной матрицей).

Смысл её такой же, как и у весовой функции скалярной системы. Элементы 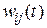матрицы являются скалярными весовыми функциями. Если j -й вход 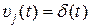, а остальные входы равны нулю, то .

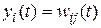Передаточная и весовая матрицы связаны между собой преобразованием Лапласа:

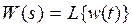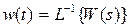, . (8.40)

Частотные характеристики системы в многомерном случае не нашли широкого применения. Хотя формально сделав в 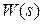замену , можно ввести аналогичные понятия и рассматривать обычных скалярных частотных характеристик .

Если уравнения (8.27) описывают одномерную систему, то 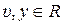, , 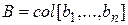. В этом случае 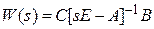, w (t) = C Ф(t) B будут скалярными функциями.

Пример 8.8. Рассмотрим систему, имеющую два входа и один выход:

, , .

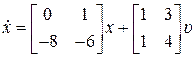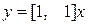В примере 8.7 найдена матрица [ sE – A ]^–1. Используя выражение
W (s) = C [ sE – A ]^–1 B, нетрудно получить передаточную матрицу размерностью 1×2 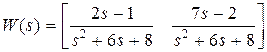. Весовая матрица будет иметь вид .

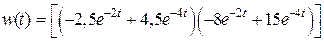Дата добавления: 2014-12-07