Переходная матрица состояния

Пусть линейная САУ описывается уравнениями состояния:

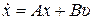, , , , . (8.27)

Рассмотрим матричный ряд, который обозначим через :

, (8.28)

где Е – единичная 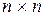матрица.

Доказано, что этот ряд абсолютно сходится при любом t к некоторой 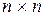матрице, обозначенной нами через (экспоненциал матрицы).

Свойства ряда (8.28):

1. При матрица .

2.

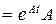, или в более общем виде .

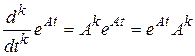3. 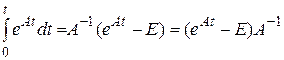, где – обратная матрица.

4. Если , то .

Рассмотрим однородное уравнение

, (8.29)

соответствующее неоднородному дифференциальному уравнению 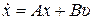, и зададим начальное состояние вектора х (0) при t = 0.

Общее решение однородного уравнения (8.29) задается выражением

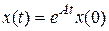. (8.30)

Действительно, подставляя (8.30) в (8.29), с учетом свойства 2 получим тождество, справедливое при любом начальном значении х (0). Это значит, что (8.30) определяет общее решение уравнения (8.29).

Введем обозначение . Матрицу 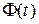размерностью 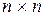будем называть переходной матрицей состояния (в математике ей соответствует фундаментальная матрица), а выражение (8.30) в этом случае будем записывать в виде

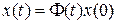. (8.31)

Выражение (8.31) можно трактовать как линейное преобразование (переход) начального значения вектора состояния х (0) в текущее значение x (t) в пространстве состояний.

Свойства переходной матрицы состояния:

1. .

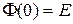2. .

3. .

Эти свойства следуют из общих свойств экспоненциала матрицы.

Если известна переходная матрица состояния, то общее решение неоднородного уравнения 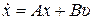записывается в виде (формула Коши)

. (8.32)

В силу получим выражение для вычисления вектора выхода y (t):

. (8.33)

В (8.32), (8.33) первое слагаемое определяет свободную составляющую, обусловленную ненулевым начальным состоянием х (0), а второе – вынужденную составляющую, обусловленную входным сигналом .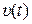

Выражение (8.28) редко употребляется для определения матрицы 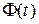, так как в случае произвольной матрицы А элементы матрицы 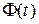представляют собой ряды Тейлора при t = 0, пo которым трудно найти исходную функцию в замкнутой форме.

Переходную матрицу состояния обычно находят с помощью операционного исчисления. Применим к (8.29) преобразование Лапласа, тогда получим , где 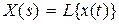. Из полученного выражения находим 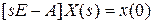, , где – обратная матрица к матрице .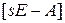

Переходя к оригиналам, имеем

. (8.34)

Сравнивая (8.34) с (8.31), приходим к выводу, что

. (8.35)

Каждый элемент матрицы есть дробно-рациональная функция переменной s. Знаменатель каждого элемента представляет собой полином n -й степени , а числитель – полином не выше (n – 1)-й степени. Полином называется характеристическим полиномом системы, а алгебраическое уравнение n -й степени

(8.36)

назовем характеристическим уравнением системы.

Применяя к каждому элементу матрицы обратное преобразование Лапласа, получим матрицу 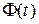, элементами которой будут некоторые функции времени.

Переходную матрицу состояний можно найти, используя модальную матрицу M. Пусть в уравнении (8.29) матрица А имеет различные собственные значения . Тогда в (8.29) сделаем замену переменных , где М – модальная матрица. В результате получим: .

Общее решение полученной системы с диагональной матрицей будет таково: . Так как , , то общее решение исходного уравнения (8.29) запишется в виде .

Отсюда следует, что

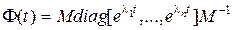. (8.37)

Пример 8.7. Рассмотрим однородное уравнение в нормальной форме:

.

Собственные числа матрицы А определяются из решения уравнения и будут , .

Ищем модальную матрицу М в виде (8.14):

, .

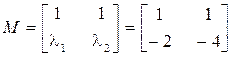Находим 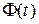в соответствии с (8.37):

.

Можно найти 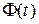, используя (8.35). Находим 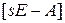и затем .

, .

Переходя от к оригиналам, найдем выражение для матрицы 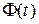, не отличающееся от полученного ранее.

Дата добавления: 2014-12-07