Корректирующие устройства по внешнему воздействию

Встречно-параллельные корректирующие устройства. Встречно-параллельные корректирующие устройства выполняются в виде местных обратных связей. Наиболее часто обратными связями охватывают силовую часть системы управления (исполнительные элементы и усилители мощности).

Рассмотрим общие свойства таких корректирующих устройств. Для рис. 9.1, в частотная характеристика участка, охватываемого обратной связью, имеет вид .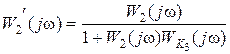

Обычно в диапазоне рабочих частот системы (в диапазоне низких частот) выполняется условие 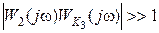и частотная характеристика , т.е. характеристика участка цепи, охваченного обратной связью, определяется только видом частотной характеристики корректирующего элемента и не зависит от звена прямой цепи 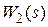. В ряде случаев это позволяет скомпенсировать нежелательное влияние звена 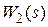на динамику системы, например, влияние малых нелинейностей или малого изменения параметров этого звена прямой цепи.

В зависимости от вида передаточной функции корректирующие обратные связи делятся на жесткие и гибкие. Если звено является статическим (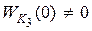), то обратная связь называется жесткой. Если звено является звеном дифференцирующего типа (), то имеем гибкую обратную связь. Жесткая обратная связь действует как в переходных, так и в установившихся режимах, а гибкая – только в переходных.

Рассмотрим несколько частных задач коррекции с помощью обратных связей.

Пусть 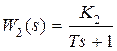, . Тогда передаточная функция участка цепи 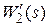, охваченного отрицательной обратной связью, будет иметь вид

, где , .

Итак, структура звена не изменилась, оно осталось апериодическим, но произошло уменьшение коэффициента передачи и эквивалентной постоянной времени 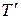. Отсюда следует, что охват в прямой цепи наиболее инерционного звена позволяет уменьшить инерционность всей цепи, что благоприятно сказывается на показателях качества системы (быстродействии, устойчивости). Уменьшение коэффициента передачи можно компенсировать введением дополнительного усилительного устройства.

Пусть , , тогда 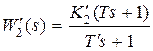, , . в этом случае меняется тип звена. При 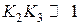, 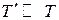и можно записать приближенное выражение для передаточной функции . Итак, получили эквивалентное форсирующее звено, влияние которого аналогично влиянию введения производной при параллельной коррекции.

Рассмотрим изменение свойств охваченного участка прямой цепи при охвате его гибкой обратной связью. Пусть , .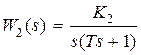

В этом случае передаточная функция участка цепи с обратной связью , где , , .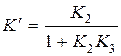

Итак, при сохранении интегрирующих свойств эквивалентная передаточная функция обладает форсирующими свойствами из-за сомножителя . Если сделать величину 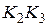достаточно большой, то малыми постоянными времен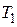и и 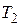можно пренебречь. При этом получим 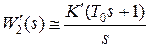, 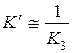. В этом случае получаем в прямой цепи изодромное звено.

Пример 9.2. Рассмотрим нескорректированную систему, как и в примере 9.1. Передаточная функция системы без коррекции будет иметь вид 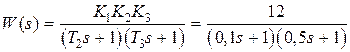. Требуется, чтобы статическая ошибка в системе при управляющем входном сигнале 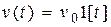, 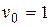не превосходила величины 0,1, т.е. 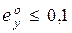, а время регулирования с.

При 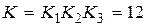статическая ошибка в системе будет 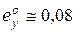, т.е. будет удовлетворять заданным требованиям.

Оценим в системе время регулирования, базируясь на корневых
оценках качества. Характеристическое уравнение замкнутой системы имеет вид

.

Это уравнение имеет два комплексных корня, действительная часть которых , откуда следует, что система устойчива. степень устойчивости системы 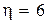и в соответствии с (7.4) с. Таким образом, время регулирования в системе не удовлетворяет заданному. Для уменьшения времени регулирования следует уменьшить максимальную постоянную времени. Для этого охватим последнее звено с передаточной функцией жесткой отрицательной обратной связью с передаточной функцией 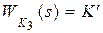, . Тогда передаточная функция скорректированного участка цепи будет

,

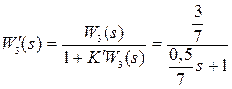а передаточная функция разомкнутой скорректированной системы будет

.

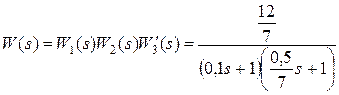Для компенсации уменьшения общего коэффициента усиления и обеспечения заданной точности в прямую цепь введем дополнительное усилительное звено с коэффициентом усиления, равным 7 (фактически это последовательная коррекция). В этом случае окончательно передаточная функция скорректированной системы , характеристическое уравнение замкнутой системы

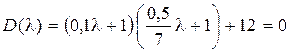
имеет два комплексных корня с действительной частью .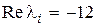

Таким образом, 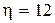, время регулирования с, и после коррекции система удовлетворяет заданным показателям качества.

При изменении передаточной функции прямой цепи с помощью последовательных, параллельных или встречно-параллельных корректирующих устройств для достижения заданных показателей качества неизменным остается главный принцип построения системы – принцип обратной связи (управление по отклонению). Учет внешнего воздействия при коррекции, в частности применение принципа компенсации (управление по возмущению) совместно с управлением по отклонению, позволяет расширить возможности коррекции системы.

Системы, использующие как управление по отклонению, так и по возмущению, относятся к классу комбинированных систем управления (см. подразд. 1.1). Наиболее часто комбинированное управление применяется для повышения точности системы управления и уменьшения установившейся ошибки. При определенных условиях с помощью комбинированного управления можно свести установившуюся ошибку к нулю при любой форме внешнего воздействия. Такое свойство называется инвариантностью системы по отношению к внешнему воздействию.

На рис. 9.5, а представлена структура комбинированной системы с корректирующим устройством по управляющему воздействию, а на рис. 9.5, б –
с корректирующим устройством по возмущению, где в первом случае передаточная функция корректирующего устройства обозначена через 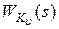, а во втором – через .

Передаточная функция замкнутой системы без коррекции, связывающая выход y со входом , для обоих случаев имеет вид

. (9.9)

Найдем связь изображений выходного сигнала y с внешними
воздействиями.

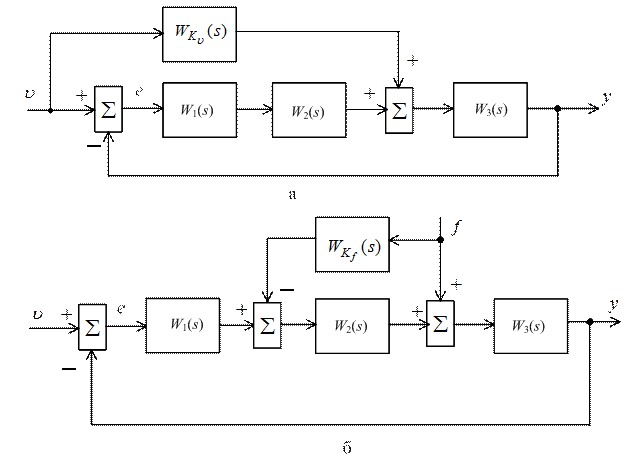
Рис. 9.5

Для структуры, изображенной на рис. 9.5, а, имеем

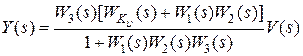, (9.10)

а для структуры на рис. 9.5, б имеем

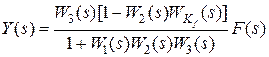. (9.11)

Задача любой системы автоматического управления – как можно более точно воспроизвести управляющий (полезный) сигнал 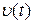и максимально ослабить влияние возмущения на выходной сигнал. С этой точки зрения желательно, чтобы в (9.10) передаточная функция, связывающая 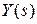и 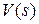, была равна единице (тогда 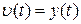), а передаточная функция в (9.11), связывающая 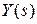и 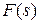, была равна нулю (тогда не влияет на ).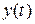

Выполнением этих условий будут соответственно следующие соотношения:

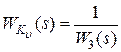, (9.12)

. (9.13)

Условия (9.12), (9.13) соответствуют так называемой полной инвариантности системы. При выполнении (9.12) передаточная функция, связывающая ошибку е и входной сигнал , как это нетрудно проверить, будет равна нулю, т.е. ошибка в системе не зависит (инвариантна) от управляющего сигнала и всегда равна нулю. При выполнении (9.13) выход системы y не зависит (инвариантен) от возмущения f.

Отметим, что условия (9.12), (9.13) гарантируют инвариантность соответствующих координат с точностью до свободной составляющей, т.е. процессы, вызванные начальными отклонениями соответствующих координат и их производных, компенсироваться не будут.

Сравнивая (9.9)–(9.11), приходим к выводу, что характеристическое уравнение нескорректированной системы (9.9) и скорректированных систем (9.10), (9.11) одно и то же:

, (9.14)

т.е. коррекция по внешнему воздействию не изменяет характеристического уравнения системы и соответственно свойств устойчивости (запасов устойчивости), а также ряда других показателей качества переходных процессов.

В силу этого контур управления по отклонению, как правило, используют для придания определенных динамических свойств системе, а контуры коррекции по внешним воздействиям – для обеспечения точности.

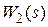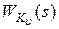Точное выполнение условий инвариантности (9.12), (9.13) практически невозможно из условий физической реализуемости. Действительно, если в (9.12), (9.13) передаточные функции , соответствуют физически реализуемым звеньям, т.е. степени полиномов относительно их числителя меньше степеней знаменателя, то передаточные функции и , обратные им, будут соответствовать физически нереализуемым звеньям.

Поэтому (9.12), (9.13) выполняются на практике с некоторой погрешностью, в силу чего и инвариантность систем будет неполной, но ошибки в системе с помощью корректирующих устройств по внешнему воздействию могут быть значительно уменьшены.

9.4. Синтез САУ на основе логарифмических частотных
характеристик

Общий порядок синтеза системы включает следующие этапы:

1. По виду передаточной функции исходной системы строится ЛАХ исходной системы 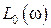. При этом исходная система должна иметь функционально необходимые элементы и должна быть минимально-фазовой.

2. На основании требований к САУ строится желаемая ЛАХ .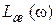

3. Путем сравнения характеристик 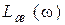и 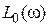определяется (если коррекция последовательная). Эту коррекцию также можно пересчитать к параллельной или встречно-параллельной.

4. По виду 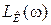определяется структурная схема и параметры
коррекции.

5. Производится моделирование системы на ЦВМ (например в среде Matlab), уточняются параметры САУ.

6. Производится реализация коррекции с помощью регуляторов или
программно.

Построение ЛАХ исходной системы не вызывает затруднений. Рассмотрим подробнее построение желаемой ЛАХ.

Учет требований точности САУ:

а) пусть даны рабочая частота 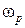и амплитуда задающего воздействия 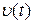, а также допустимая ошибка .

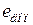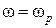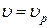
Так как для низких частот , то при , . Тогда

. (9.15)

б) пусть даны . Тогда

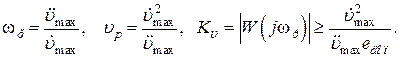(9.16)

в) Пусть для астатической САУ даны 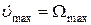и .

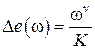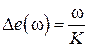Тогда и при и

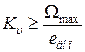. (9.17)

С помощью выражений (9.15)–(9.17) строится низкочастотная область 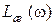(рис. 9.6).

Рис. 9.6

Значение частоты 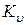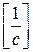называют добротностью САУ по скорости. Первый излом 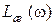на частоте при однократном изломе (при изменении наклона на 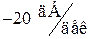) определяется как 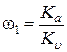, где 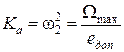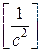называют добротностью системы по скорости; при двукратном изломе .

Учет требований качества переходного процесса: , колебатель-
ности, запасов устойчивости. Эти показатели учитываются при формировании среднечастотной области 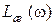. Здесь можно воспользоваться графиками (рис. 9.7, а, б).

Рис. 9.7

По графику (см. рис. 9.7, а) для заданных значени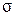й и 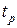находят и затем из соотношения 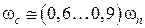частоту среза .

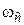Например: (как показано на рис. 9.7, а) для , , 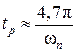откуда для заданного значения 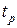(допустим, что оно равно 0,01 с), определяются значения и

По графику (см. рис. 9.7, б), где установлены зависимости 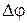от 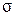и ординат и среднечастотной части 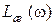от 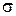, находят для заданного значения 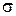необходимые 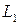, 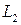и .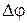

Сопряжение среднечастотного участка с низкочастотным и высокочастотным (рис. 9.8) должно быть таким, чтобы была проще коррекция и изломы, по возможности, были однократными.

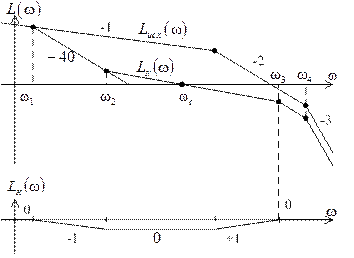
Рис. 9.8

Для облегчения процедуры синтеза коррекции вводятся типовые передаточные функции исходной системы и соответствующие им передаточные функции желаемой системы:

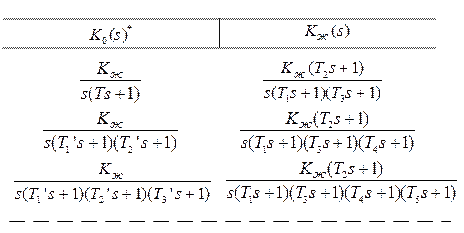
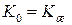* с учётом требований по точности;

Остановимся на коррекции. Вычитая из 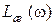ординаты 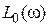, получим Вид ЛАХ коррекции соответствует случаю коррекции с опережением и отставанием по фазе.

Передаточная функция коррекции будет с учётом обеспечения показателей точности иметь вид

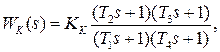(9.18)

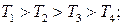
где 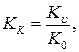причём 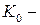коэффициент передачи исходной системы.

Так как реализовать дифференцирующие звенья сложно, переходят к схеме коррекции с использованием интеграторов. Для этого необходимо представить (9.18) в виде

Схема реализации коррекции представлена на рис. 9.9.

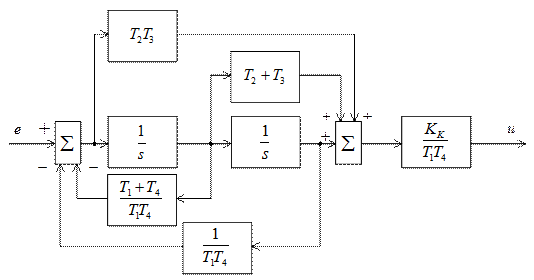
Рис. 9.9

Дата добавления: 2014-12-07