V. Политропные процессы

IV. Адиабатный процесс

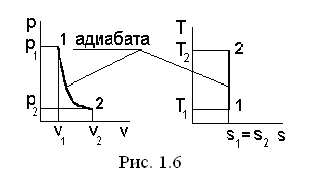
Адиабатный процесс протекает без теплообмена с окружающей средой, при соблюдении условия dq=0. Из выражения (1.8) при условии dq=0, следует , т.е. теплоемкость адиабатного процесса с=0.

Из (1.1) 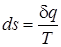вытекает, что ds=0, s=const. Следовательно, в адиабатном процессе энтропия не изменяется. В соответствии с выражением , показатель политропы при адиабатном процессе будет равен 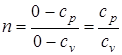, который обозначается 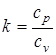, как было отмечено выше, и называется показателем адиабаты. Уравнение, описывающее адиабатный процесс, имеет вид p·v^k=const, из которого следует .

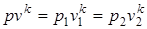Перечень величин (1.37) при адиабатном процессе должен удовлетворять следующим соотношениям

; (1.59)

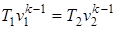; (1.60)

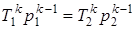; (1.61)

l_1-2=u₁ - u₂ ; (1.62)

; (1.63)

Du= u₂ - u₁ =c_v(T₂ - T₁); (1.64)

Dh= h₂ - h₁ =c_p(T₂ - T₁); (1.65)

Ds= s₂- s₁ =0, s₂= s₁. (1.66)

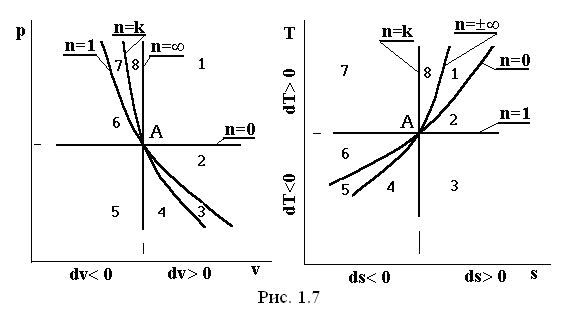
Выше было отмечено, что термодинамические процессы, которые описываются уравнением p×vⁿ= const, называются политропными. В этом уравнении показатель политропы меняется в пределах -¥< n< +¥. Представим объединенную картину линий изопараметрических процессов в pv-, Ts -диаграммах, приняв за начало всех процессов (как в сторону расширения, так и в сторону сжатия) произвольную точку А. На этом рисунке приведены соответственно: изохора (n= ±¥), изобара (n=0), изотерма (n=1), адиабата (n=k). Эти изолинии делят координатную плоскость на 8 областей, в пределах каждой из которых все термодинамические процессы обладают общностью определенных свойств. Все процессы, начинающиеся в точке А, и происходящие в областях 1, 2, 3, 4, сопровождаются расширением рабочего тела (dv>0), следовательно, при этом совершается положительная работа δl=p×dv, а процессы, происходящие в областях 5, 6, 7 и 8 (dv<0), имеют отрицательную работу (в этих случаях работа совершается над системой внешними силами).

Процессы, совершающиеся в областях 1, 2, 3 и 8, протекают с подводом теплоты извне (ds>0), а в областях 4, 5, 6 и 7 - с отводом теплоты (ds<0).

Изотерма (n=1) делит рассматриваемое поле координатной плоскости на две части: в областях 1, 2, 7, 8 процессы протекают с повышением температуры (dT>0), а в областях 3, 4, 5, 6 процессы протекают с понижением температуры (dT<0). В области 3 между изотермой (n=1) и адиабатой (n=k) при подводе теплоты (ds>0), происходит падение температуры (dT<0), а при отводе теплоты (ds<0) в области 7 происходит повышение температуры (dT>0).

Все соотношения, вытекающие из уравнений политропных процессов p×vⁿ= const; T×v^n-1= const; Tⁿ×p^1-n= const, должны быть аналогичными соотношениям, вытекающим из соответствующих уравнений адиабатного процесса и получаются путем замены показателя адиабаты k на показатель политропы n. Однако при этом необходимо иметь в виду, что теплоемкость политропного процесса определяется по формуле 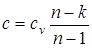, а также теплота, участвующая в процессе, в этом случае определяется исходя из уравнения первого закона термодинамики

.

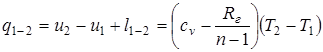Перечень величин (1.37) в политропном процессе должен удовлетворять следующим соотношениям

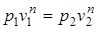; (1.67)

; (1.68)

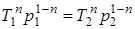; (1.69)

; (1.70)

Du= u₂ - u₁ =c_v× (T₂- T₁); (1.71)

Dh= h₂ - h₁ =c_p× (T₂- T₁); (1.72)

; (1.73)

; (1.74)

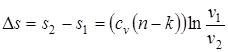; (1.75)

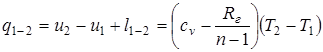. (1.76)

Дата добавления: 2014-12-07