Комплексные спектры единичных скачков в соответствии с теоремой о запаздывании

Предварительно умножаем её на множитель сходимости и для

Мат. модель его – функция 1(t) – абсолютно не интегрируется.

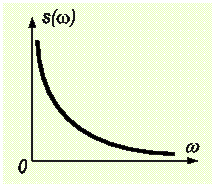
Спектр единичного скачка

Амплитуды гармоник в спектре амплитуд всегда положительны. Поэтому после частоты 2p/tпри каждом спаде огибающей до нуля огибающая должна менять знак, что соответствует приращению наpначальной фазы гармоники.

промежуточного экспоненциального сигнала –

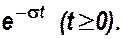
находим спектр

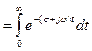
Комплексный спектр сигнала единичного скачка

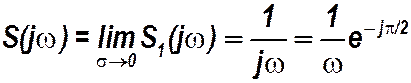
Спектр амплитуд - S( w )=1/ w сплошной (гипербола).

Спектр единичного скачка - S(j w ) = 1/j w = (1/ w) e^{- j p /2}.

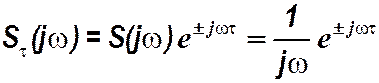, а спектр амплитуд неизменен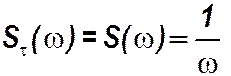

Другой вариант расчёта спектра прямоугольного импульса

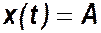
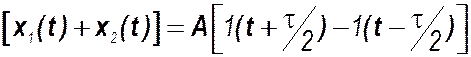
Спектр единичного скачка 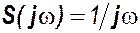. Согласно теореме о запаздывании сигнала спектры сигналов х₁ и х₂ будут

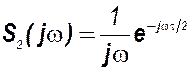
Тогда на основании теорем о сумме спектров и о смещении сигнала спектр прямоугольного импульса находится как разность спектров неединичных скачков:

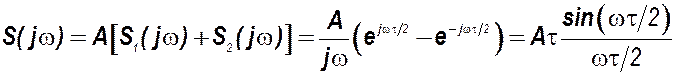
Комплексный спектр единичного импульса

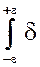S( j w ) = (t) e^{-j w t}dt = (t)e^{-j w t}dt = e^{-j w 0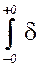} (t) dt = 1,

и совпадает со своим модулем: | S( j w ) | = S( w ) = 1. Спектр амплитуд - сплошной, простирающийся до бесконечно больших значений -w и +w с неизменной спектральной плотностью при всех частотах, равной 1.

Если бесконечный спектр d-сигнала ограничить частотой среза w_с (как показано на рис.), то единичный импульс принимает вид сигнала, описываемого функцией вида sin w _сt/ w _сt. Её называют во многих литературных источниках функцией отсчётов и обозначают Sa( a ). Такая функция равна 1 при a=0 (при нулевом аргументе), а с увеличением a изменяется по закону затухающего синуса

Другой вариант – расчёт спектра одиночного прямоугольного импульса с длительностью t и площадью, равной 1.

Дата добавления: 2014-12-07