Властивості ймовірностей подій

1. Ймовірність любої події заключна між нулем і одиницею, тт.

2. Ймовірність вірогідної події дорівнює одиниці.

3. Ймовірність неможливої події дорівнює нулю.

Статистичною ймовірністю події А називається відносна частота появи цієї події в 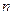проведених випробуваннях, тт.

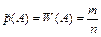, (1.2)

де – статистична ймовірність події 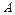; 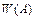– відносна частота події 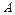; 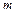– число іспитів, в яких з’явилась подія 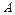; 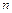– загальне число іспитів.

Приклад 1.2. По цілі зроблено 20 пострілів, причому зафіксовано 18 влучень. Знайти відносну частоту влучень в ціль.

Розв’язання. Нехай подія А – влучення в ціль. Всього було зроблено 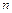=20 пострілів, з них 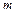=18 влучень. Тоді відносна частота влучень в ціль за формулою (1.2) дорівнює .

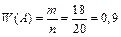Одним з недоліків класичного означення ймовірності, обмежуючим його застосування, є те, що воно передбачає кінцеве число можливих результатів випробувань.

Якщо позначити міру (довжину, площу, об’єм) області через mes, то геометричною ймовірністю події А називається відношення міри області сприятливої появі події А до міри усієї області, тт.

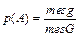, (1.3)

де g – фігура, сприятлива появі події А; G – фігура, на яку навмання кидається точка.

Приклад 1.3. Два лиця А і В домовилися зустрітися в визначеному місці, при цьому кожний з’являється туди в любий момент часу між 11 і 12 годинами і дожидає на протязі 20 хвилин. Якщо партнер до цього часу ще не прийшов або вже покинув домовлене місце, зустріч не відбулася. Знайти ймовірність того, що зустріч відбудеться.

Розв’язання. Позначимо моменти приходу в визначене місце лиць А і В через 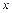і 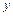. В прямокутній системі координат 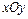візьмемо за початок відліку 11 годин, а за одиницю вимірювання –1 год. За умовою , 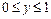. Цим нерівностям

задовольняють координати любої точки, що належить

квадрату 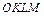зі стороною 1. Нехай подія – зу-

стріч двох лиць – відбудеться, якщо різниця між 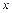і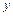

не перевищує 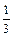часу (по абсолютній величині), тт.

. Розв’язком останньої нерівності є смуга

, що знаходиться в середині квадрата (площа g) (рис.1). За формулою (13) маємо

.

Площа g дорівнює площі квадрата без суми площ двох кутових не замальованих трикутників.

Дата добавления: 2014-12-07