Інтегральна теорема Муавра-Лапласа

Локальна теорема Муавра-Лапласа

Якщо ймовірність появи події 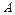в кожнім іспиті стала і відмінна від нуля і одиниці, то ймовірність

, (1.23)

де і .

Функція – парна , монотонно спадна (при ) і обчислюється за таблицею1 (Додаток 1).

Якщо ймовірність появи події 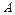в кожному іспиті стала і відмінна від нуля і одиниці, то ймовірність того, що подія 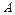з’явиться в 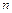іспитах від до 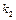разів, наближено дорівнює

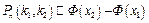, (1.24)

де і , .

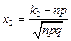Функція Лапласа Ф(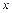) – непарна (Ф(- 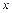))= – Ф(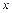), монотонно зростаюча (при 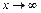, Ф 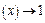) і обчислюється за таблицею додатку 2.

Наближені формули Муавра-Лапласа застосовують практично у випадках коли і не малі а [1]. При цій умові формули (1.23) і (1.24) дають незначні похибки обчислення ймовірностей.

Приклад 1.18. В деякій місцевості на кожні 100 сімей припадає 80 холодильників. Знайти ймовірність того, що з 400 сімей: а) 300 сімей мають холодильники; б) від 320 до 350 сімей (включно) мають холодильники.

Розв’язання. Ймовірність того, що сім’я має холодильник . Перевіримо умову застосування формул (1.23) і (1.24.)

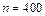, , , тоді .

Отже, теоремами Муавра-Лапласа можна користуватися.

а) Скориставшись локальною теоремою Муавра-Лапласа. Спочатку визначимо 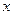, враховуючи, що 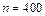, , , , тоді

Користуючись додатком 1 позначенню знайдемо , врахувавши парність .

Отже, за формулою (1.23) маємо: .

б) За умовою , , , , .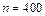

Визначимо 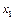і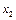

,

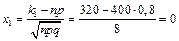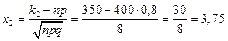
Ф(0)=0, Ф(3,75)=0,499890005-0 0,5

Отже, за формулою (1.24) маємо

.

Дата добавления: 2014-12-07