Повторення випробувань

Формули Бейеса дозволяють переоцінювати ймовірності гіпотез після того, як становиться відомим результат випробування, в якому з’являється подія А.

Приклад 1.15. До взуттєвої майстерні для ремонту приносять чоботи і туфлі у співвідношенні 2:3. Ймовірність якісного ремонтування чобіт дорівнює 0,9, а туфель – 0,85. Проведена перевірка якості однієї пари взуття. Виявилося, що ця пара взуття відремонтована якісно. Яка ймовірність того, що це: а) чоботи; б) туфлі.

Розв’язання. Нехай подія А – принесене взуття відремонтовано якісно. Позначимо подію – до ремонту принесли чоботи, 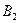– до ремонту принесли туфлі.

Отже, ймовірності гіпотез , .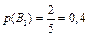

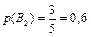Умовні ймовірності відповідно дорівнюють

;

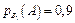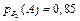
Тоді:

а) ймовірність того, що відремонтованим якісно взуттям є чоботи буде

;

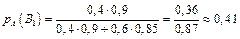б) ймовірність того, що відремонтованим якісно взуттям є туфлі буде

.

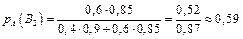Якщо ймовірність появи події А в кожному випробуванні не змінюється в залежності від результатів інших, то такі випробування називаються незалежними відносно події А. Якщо незалежні повторні випробування проводяться при одному й тому ж комплексі умов, то ймовірність появи події А в кожному випробуванні одна й та ж.

Така послідовність незалежних випробувань отримала назву схеми Бернуллі.

Формула Бернуллі. Ймовірність того, що в 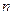незалежних випробуваннях, у кожнім з яких ймовірність події дорівнює 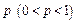, подія з’явиться рівно 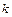разів (байдуже в якій послідовності) дорівнює:

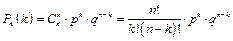, (1.21)

де .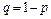

Ця формула відображує біномний розподіл ймовірностей.

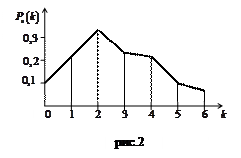
Якщо отримані ймовірності зобразити графічно точками з координатами 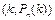, то з’єднуючи ці точки отримаємо многокутник або полігон розподілу ймовірностей (рис.2). Використовуючи многокутник розподілу можна стверджувати, що існують такі значення 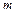при яких ймовірність буде найбільшою. Число 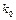появи події А в 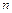незалежних випробуваннях називається найімовірнішим, якщо ймовірність здійснення цієї події при любім .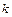

в) якщо число 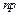– ціле, то найімовірніше число .

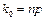Приклад 1.16. Батарея зробила 14 пострілів по об’єкту, ймовірність влучень в який при кожному пострілі дорівнює 0,2. Знайти найімовірніше число влучень і ймовірність цього числа влучень.

Розв’язання. За умовою 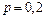, тоді 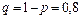, 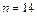. Використавши формулу (1.22), отримаємо

.

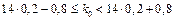
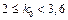Оскільки число 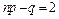– ціле, то існує два найімовірніших числа 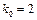і .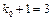

Тепер використавши формулу (1.21) обчислимо ймовірність числа влучень

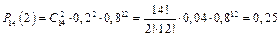
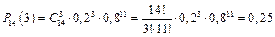
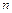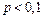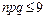У випадку, коли велике, а мале (так згідно з [3] ; , а згідно з [1] 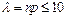) маємо справу з рідкісними масовими явищами, замість формули (1.21) користуються наближеною формулою Пуассона:

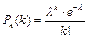(1.22)

Приклад 1.17. В новому мікрорайоні поставлено 10000 кодових замків на вхідних дверях будинків. Ймовірність виходу зі строю одного замка на протязі місяця дорівнює 0,0002. Знайти ймовірність того, що за місяць відкажуть три замка.

Розв’язання. За умовою , , .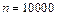

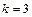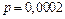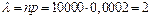
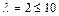, отже, можна примінити формулу Пуассона (1.22)

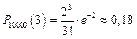
Користуватися формулою Бернуллі при великих значеннях 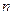достатньо важко, оскільки формула потребує виконання дій над громіздкими числами. Тому для наближеного (асимптотичного) обчислення ймовірностей

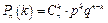і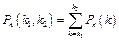

в 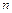незалежних випробуваннях Бернуллі при великих 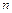, , 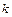, 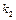використовують теореми Муавра-Лапласа.

Дата добавления: 2014-12-07