Властивості щільності ймовірностей

1. Щільність ймовірності невід’ємна функція, тт.

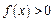
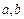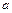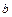2. Ймовірність попадання неперервної випадкової величини в інтервал [ ] дорівнює визначеному інтегралу від її щільності ймовірності в межах від до , тт.

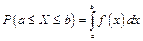(1.32)

3. Функція розподілу неперервної випадкової величини може бути записана через щільність за формулою

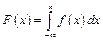(1.33)

4. Невласний інтеграл в нескінченних межах від щільності ймовірності неперервної випадкової величини дорівнює одиниці:

.

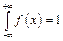Приклад 1.24. Щільність ймовірності неперервної випадкової величини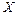

.

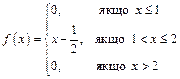Знайти функцію розподілу 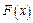і побудувати графіки 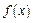і .

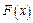Розв’язання. Використовуючи формулу (1.33) для кожного з інтервалів знайдемо .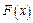

1). Якщ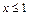о , то 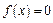, отже

.

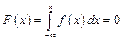2). Якщо 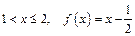, отже

.

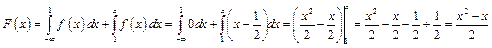3). Якщо 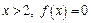, отже

.

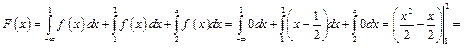
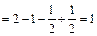Таким чином функція розподілу має вигляд:

.

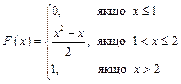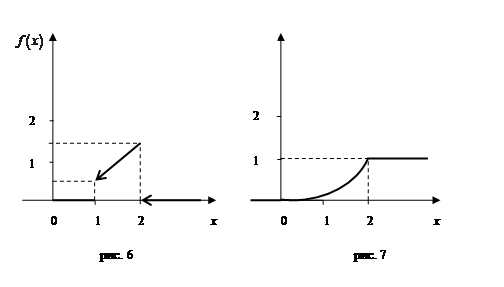Будуємо графіки функцій 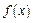і 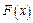(рис. 6 і рис. 7).

Математичним сподіванням неперервної випадкової величини Х, можливі значення якої належать відрізку 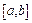, називають визначений інтеграл

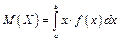(1.34)

Якщо можливі значення належать до усієї осі 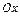, то

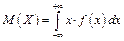(1.34')

Дисперсією неперервної випадкової величини називають математичне сподівання квадрата її відхилення.

Якщо можливі значення Х належать відрізку 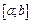, то

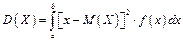, (1.35)

якщо можливі значення належать до усієї осі 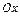, то

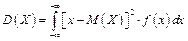. (1.35')

Зауваження. Для обчислення дисперсії неперервної випадкової величини можна використовувати більш зручні формули

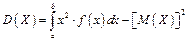(1.36)

або

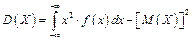. (1.36')

Середнє квадратичне відхилення неперервної випадкової величини визначається як і для величини дискретної рівністю

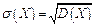(1.37)

Приклад 1.25. Дана інтегральна функція:

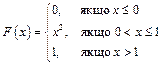
Знайти: математичне сподівання, дисперсію, середнє квадратичне відхилення.

Розв’язання. Знайдемо спочатку диференціальну функцію:

.

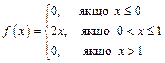Обчислимо математичне сподівання за формулою (1.34)

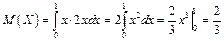
дисперсію за формулою (1.36):

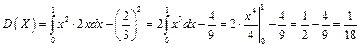
середнє квадратичне відхилення за формулою (1.37):

.

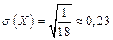Модою 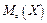випадкової величини 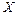називається її найбільш вірогідне значення (при якому ймовірність 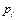або щільність ймовірності 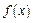досягає максимуму).

Медіаною 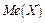неперервної випадкової величини 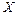називається таке її значення, для якого

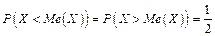(1.38)

Приклад 1.26. Знайти моду, медіану і математичне сподівання випадкової величини Х, яка задана щільністю ймовірності

.

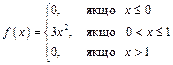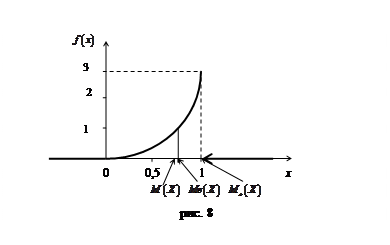
Розв’язання. Крива розподілу представлена на рис. 8

Очевидно, що щільність ймовірності 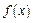максимальна при 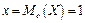. Медіану 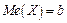знайдемо з умови

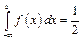
або

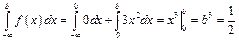
звідки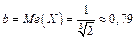

Математичне сподівання обчислюємо за формулою (1.34')

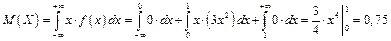
Взаємне розташування точок 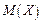, 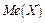і 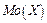в порядку зростання абсцис вказано на рис.8.

Дата добавления: 2014-12-07