Розв’язання типового варіанта. 1.Знайти невизначені інтеграли

1. Знайти невизначені інтеграли

а) 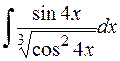; б) в) .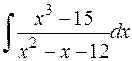

►а) Застосуємо метод підстановки. Нехай t =cos4 x, тоді dt =-4sin xdx. Замінивши підінтегральний вираз, маємо

.

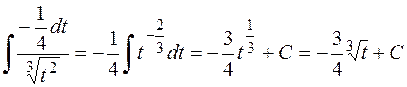Повертаючись до старої змінної, маємо

.

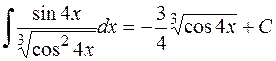б) Застосуємо метод інтегрування частинами

(11.15)

Нехай

U = arctg x, dV =2 xdx.

Тоді

dU = ; V = .

Використовуючи формулу (11.15), маємо

- .

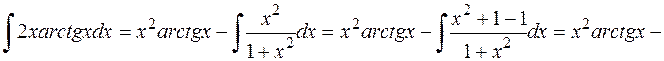
в) Підінтегральна функція є неправильним раціональним дробом. Вилучивши цілу частину, тобто поділивши чисельник цього дробу на знаменник, маємо:

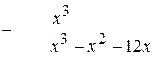
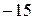
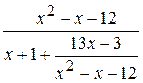
Отже,

.

Подамо правильний раціональний дріб у вигляді суми найпро-стіших раціональних дробів.

.

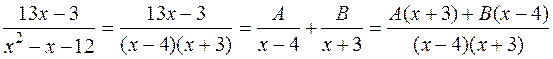Порівняння чисельників дає

13 x -3=A(x +3)+B(x -4).

Звідси при x = -3 маємо -39 - 3 = -7B; 7B = 42, B = 6;

при х = 4 маємо 52 -3 = 7А, 7А = 49, А = 7.

Отже,

.

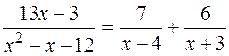Таким чином, отримаємо:

= .◄

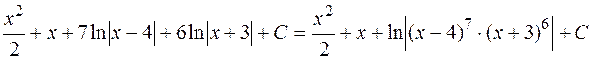2. Обчислити визначений інтеграл

.

► Застосуємо метод заміни змінної. Нехай , тоді

3 + ln x = t ²,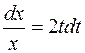

Визначимо межі інтегрування для змінної t.

Якщо x = 1, то t = 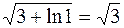- нижня межа

Якщо x = е, то t = -верхня межа.

Таким чином,

◄

3. Обчислити площу фігури, що обмежена параболою y = x ² -3 x та прямою y = 4 -3 x.

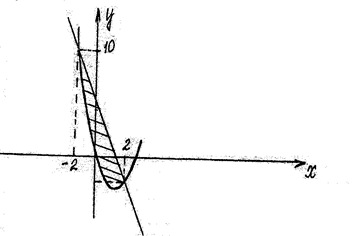
Рис. 6.

► Площа фігури, обмеженої згори графіком функції y = f (x), знизу – графіком функції y = g (x), зліва та справа, відповідно, прямими x = а, x = b, визначається формулою:

dx. (11.16)

Визначимо точки перетину параболи та прямої, розв’язавши для цього систему рівнянь

Враховуючи, що у формулі (11.16) f (x) = 4 -3 x, g(x) = x ² -3 x; a = -2; b = 2, маємо наступний вираз для визначення площі:

S= .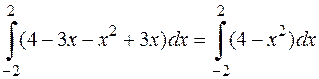

Під знаком визначеного інтеграла парна функція. Користуючись формулою

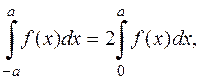
маємо

(кв.од.).◄

Дата добавления: 2014-11-29